
【題目】已知函數f(x)=![]() ,把方程f(x)-x=0的根按從小到大順序排成一個數列,則該數列的前n項和Sn=_________。
,把方程f(x)-x=0的根按從小到大順序排成一個數列,則該數列的前n項和Sn=_________。
【答案】![]()
【解析】解答:
當![]() 時,有
時,有![]() ,則
,則![]() ,
,
當![]() 時,有
時,有![]() ,則
,則![]() ,
,
當![]() 時,有
時,有![]() ,則
,則![]() ,
,
當![]() 時,有
時,有![]() ,則
,則![]() ,
,
以此類推,當![]() (其中
(其中![]() )時,則
)時,則![]() ,
,
所以,函數![]() 的圖象與直線
的圖象與直線![]() 的交點為:(0,1)和(1,2),
的交點為:(0,1)和(1,2),
由于指數函數![]() 為增函數且圖象下凸,故它們只有這兩個交點。
為增函數且圖象下凸,故它們只有這兩個交點。
然后①將函數![]() 和y=x+1的圖象同時向下平移一個單位,即得到函數
和y=x+1的圖象同時向下平移一個單位,即得到函數![]() 和
和![]() 的圖象,
的圖象,
取![]() 的部分,可見它們有且僅有一個交點(0,0).
的部分,可見它們有且僅有一個交點(0,0).
即當![]() 時,方程
時,方程![]() 有且僅有一個根x=0.
有且僅有一個根x=0.
②取①中函數![]() 和
和![]() 圖象
圖象![]() 的部分,再同時向上和向右各平移一個單位,
的部分,再同時向上和向右各平移一個單位,
即得![]() 和y=x在0<x1上的圖象,此時它們仍然只有一個交點(1,1).
和y=x在0<x1上的圖象,此時它們仍然只有一個交點(1,1).
即當0<x1時,方程f(x)x=0有且僅有一個根x=1.
③取②中函數![]() 和y=x在0<x1上的圖象,繼續按照上述步驟進行,
和y=x在0<x1上的圖象,繼續按照上述步驟進行,
即得到![]() 和y=x在1<x2上的圖象,此時它們仍然只有一個交點(2,2).
和y=x在1<x2上的圖象,此時它們仍然只有一個交點(2,2).
即當1<x2時,方程f(x)x=0有且僅有一個根x=2.
④以此類推,函數y=f(x)與y=x在(2,3],(3,4],…,(n,n+1]上的交點依次為(3,3),(4,4),…(n+1,n+1).
即方程f(x)x=0在(2,3],(3,4],…(n,n+1]上的根依次為3,4,…,n+1.
綜上所述方程f(x)x=0的根按從小到大的順序排列所得數列為:
0,1,2,3,4,…,
∴該數列的前n項和![]() ,n∈N+.
,n∈N+.
故答案為: ![]() .
.


科目:高中數學 來源: 題型:
【題目】假設乒乓球團體比賽的規則如下:進行5場比賽,除第3場為雙打外,其余各場為單打,參賽的每個隊選出3名運動員參加比賽,每個隊員打兩場,且第1,2場與第4,5場不能是某個運動員連續比賽.某隊有4名乒乓球運動員,其中 ![]() 不適合雙打,則該隊教練安排運動員參加比賽的方法共有種
不適合雙打,則該隊教練安排運動員參加比賽的方法共有種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的首項a1=3,且公差d≠0,其前n項和為Sn , 且a1 , a4 , a13分別是等比數列{bn}的b2 , b3 , b4 . (Ⅰ)求數列{an}與{bn}的通項公式;
(Ⅱ)證明 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場欲經銷某種商品,考慮到不同顧客的喜好,決定同時銷售A、B兩個品牌,根據生產廠家營銷策略,結合本地區以往經銷該商品的大數據統計分析,A品牌的銷售利潤y1與投入資金x成正比,其關系如圖1所示,B品牌的銷售利潤y2與投入資金x的算術平方根成正比,其關系如圖2所示(利潤與資金的單位:萬元). 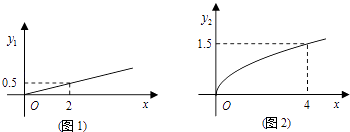
(1)分別將A、B兩個品牌的銷售利潤y1、y2表示為投入資金x的函數關系式;
(2)該商場計劃投入5萬元經銷該種商品,并全部投入A、B兩個品牌,問:怎樣分配這5萬元資金,才能使經銷該種商品獲得最大利潤,其最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足an=2an-1-2n+5,(n∈N且n≥2),a1=1,
(I)若bn=an-2n+1,求證數列{bn}(n∈N*)是常數列,并求{an}的通項;
(II)若Sn是數列{an}的前n項和,又cn=(-1)nSn,且{Cn}的前n項和Tn>tn2在n∈N*時恒成立,求實數t的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商區停車場臨時停車按時段收費,收費標準為:每輛汽車一次停車不超過1小時收費6元,超過1小時的部分每小時收費8元(不足1小時的部分按1小時計算).現有甲、乙二人在該商區臨時停車,兩人停車都不超過4小時. (Ⅰ)若甲停車1小時以上且不超過2小時的概率為 ![]() ,停車付費多于14元的概率為
,停車付費多于14元的概率為 ![]() ,求甲停車付費恰為6元的概率;
,求甲停車付費恰為6元的概率;
(Ⅱ)若每人停車的時長在每個時段的可能性相同,求甲、乙二人停車付費之和為36元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的可導函數f(x)的導函數為f′(x),滿足f′(x)>f(x),且f(x+2)為奇函數,f(4)=﹣1,則不等式f(x)<ex的解集為( )
A.(﹣2,+∞)
B.(0,+∞)
C.(1,+∞)
D.(﹣∞,0)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com