
(本題滿分14分)
醫(yī)學(xué)上為研究某種傳染病傳播過程中病毒細(xì)胞的發(fā)展規(guī)律及其預(yù)防,將病毒細(xì)胞注入一只小白鼠體內(nèi)進(jìn)行實(shí)驗(yàn),經(jīng)檢測,病毒細(xì)胞在體內(nèi)的總數(shù)與天數(shù)的關(guān)系記錄如下表.已知該種病毒細(xì)胞在小白鼠體內(nèi)的個(gè)數(shù)超過 的時(shí)候小白鼠將死亡.但注射某種藥物,將可殺死此時(shí)其體內(nèi)該病毒細(xì)胞的
的時(shí)候小白鼠將死亡.但注射某種藥物,將可殺死此時(shí)其體內(nèi)該病毒細(xì)胞的 .
.
(Ⅰ) 為了使小白鼠在實(shí)驗(yàn)過程中不死亡,第一次最遲應(yīng)在何時(shí)注射該種藥物?(精確到天)
(Ⅱ)第二次最遲應(yīng)在何時(shí)注射該種藥物,才能維持小白鼠的生命?(精確到天)
(參考數(shù)據(jù): ,
, )
)
(Ⅰ)27天
(Ⅱ)再經(jīng)過6天必須注射藥物,即第二次應(yīng)在第33天注射藥物
解析(Ⅰ)由題意病毒細(xì)胞總數(shù) 關(guān)于時(shí)間
關(guān)于時(shí)間 的函數(shù)關(guān)系式為
的函數(shù)關(guān)系式為 (其中
(其中 ), …3分
), …3分
則由 ,兩邊取常用對數(shù)得
,兩邊取常用對數(shù)得 ,從而
,從而 …6分
…6分
即第一次最遲應(yīng)在第27天注射該種藥物. ……………………………7分
(Ⅱ)由題意注入藥物后小白 鼠體內(nèi)剩余的病毒細(xì)胞為
鼠體內(nèi)剩余的病毒細(xì)胞為 , …………8分
, …………8分
再經(jīng)過 天后小白鼠體內(nèi)病毒細(xì)胞為
天后小白鼠體內(nèi)病毒細(xì)胞為 ,………………10分
,………………10分
由題意 , ………………………11分
, ………………………11分
兩邊取常用對數(shù)得 ,解得
,解得 ……………13分
……………13分
故再經(jīng)過6天必須注射藥物,即第二次應(yīng)在第33天注射藥物.………………14分



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
20.已知函數(shù)
(1)求函數(shù) 的極值;
的極值;
(2)設(shè)函數(shù) 若函數(shù)
若函數(shù) 在
在 上恰有兩個(gè)不同零點(diǎn),求實(shí)數(shù)
上恰有兩個(gè)不同零點(diǎn),求實(shí)數(shù)  的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分 分)
分)
已知函數(shù) .(
.( 為常數(shù),
為常數(shù), )
)
(Ⅰ)若 是函數(shù)
是函數(shù) 的一個(gè)極值點(diǎn),求
的一個(gè)極值點(diǎn),求 的值;
的值;
(Ⅱ)求證:當(dāng) 時(shí),
時(shí), 在
在 上是增函數(shù);
上是增函數(shù);
(Ⅲ)若對任意的 ,總存在
,總存在 ,使不等式
,使不等式 成立,求實(shí)數(shù)
成立,求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分16分)
已知函數(shù) (
( ∈R且
∈R且 ),
), .
.
(Ⅰ)若 ,且函數(shù)
,且函數(shù)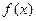 的值域?yàn)閇0, +
的值域?yàn)閇0, + ),求
),求 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的條件下,當(dāng)x∈[-2 , 2 ]時(shí), 是單調(diào)函數(shù),求實(shí)數(shù)k的取值范圍;
是單調(diào)函數(shù),求實(shí)數(shù)k的取值范圍;
(Ⅲ)設(shè) ,
, , 且
, 且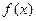 是偶函數(shù),判斷
是偶函數(shù),判斷 能否大于零?
能否大于零?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分13分)
某旅游景區(qū)的觀景臺P位于高(山頂?shù)缴侥_水平面M的垂直高度PO)為2km的山峰上,山腳下有一段位于水平線上筆直的公路AB,山坡面可近似地看作平面PAB,且△PAB為等腰三角形.山坡面與山腳所在水平面M所成的二面角為α(0°<α<90°),且sinα=.現(xiàn)從山腳的水平公路AB某處C0開始修建一條盤山公路,該公路的第一段、第二段、第三段…,第n-1段依次為C0C1,C1C2,C2C3,…,Cn-1Cn(如圖所示),且C0C1,C1C2,C2C3,…,Cn-1Cn與AB所成的角均為β,其中0<β<90°,sinβ=.試問:
(1)每修建盤山公路多少米,垂直高度就能升高100米.若修建盤山公路至半山腰(高度為山高的一半),在半山腰的中心Q處修建上山纜車索道站,索道PQ依山而建(與山坡面平行,離坡面高度忽略不計(jì)),問盤山公路的長度和索道的長度各是多少?
(2)若修建xkm盤山公路,其造價(jià)為 a萬元.修建索道的造價(jià)為2a萬元/km.問修建盤山公路至多高時(shí),再修建上山索道至觀景臺,總造價(jià)最少.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(滿分16分)
記函數(shù)f(x)的定義域?yàn)镈,若存在 ,使
,使 成立,則稱以
成立,則稱以 為坐標(biāo)的點(diǎn)為函數(shù)
為坐標(biāo)的點(diǎn)為函數(shù) 圖象上的不動點(diǎn)。
圖象上的不動點(diǎn)。
(1)若函數(shù) 的圖象上有兩個(gè)關(guān)于原點(diǎn)對稱的不動點(diǎn),求
的圖象上有兩個(gè)關(guān)于原點(diǎn)對稱的不動點(diǎn),求 應(yīng)滿足的條件;
應(yīng)滿足的條件;
(2)下述結(jié)論“若定義在R上的奇函數(shù)f(x)的圖象上存在有限個(gè)不動點(diǎn),則不動點(diǎn)有奇數(shù)個(gè)”是否正確?若正確,請給予證明,并舉出一例;若不正確,請舉出一反例說明
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)已知函數(shù)
(1)當(dāng) 時(shí),求函數(shù)
時(shí),求函數(shù) 在
在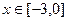 的值域;
的值域;
(2)若關(guān)于 的方程
的方程 有解,求
有解,求 的取值范圍
的取值范圍
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com