
【題目】函數![]() 的定義域為
的定義域為![]() ,對給定的正數
,對給定的正數![]() ,若存在閉區間
,若存在閉區間![]() ,使得函數
,使得函數![]() 滿足:①
滿足:①![]() 在
在![]() 內是單調函數;②
內是單調函數;②![]() 在
在![]() 上的值域為
上的值域為![]() ,則稱區間
,則稱區間![]() 為
為![]() 的
的![]() 級“理想區間”.下列結論錯誤的是( )
級“理想區間”.下列結論錯誤的是( )
A. 函數![]() (
(![]() )存在1級“理想區間”
)存在1級“理想區間”
B. 函數![]() (
(![]() )不存在2級“理想區間”
)不存在2級“理想區間”
C. 函數![]() (
(![]() )存在3級“理想區間”
)存在3級“理想區間”
D. 函數![]() ,
, ![]() 不存在4級“理想區間”
不存在4級“理想區間”
【答案】D
【解析】A中,當x0時,f(x)=x2在[0,1]上是單調增函數,且f(x)在[0,1]上的值域是[0,1],
∴存在1級“理想區間”,原命題正確;
B中,當x∈R時,f(x)=ex在[a,b]上是單調增函數,且f(x)在[a,b]上的值域是[ea,eb],
∴不存在2級“理想區間”,原命題正確;
C中,因為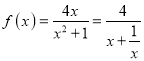 在(0,1)上為增函數。
在(0,1)上為增函數。
假設存在[a,b](0,1),使得f(x)∈[3a,3b]則有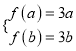 ,所以命題正確;
,所以命題正確;
D中,不妨設a>1,則函數在定義域內為單調增函數,
若存在“4級理想區間”[m,n],
則由m,n是方程tanx=4x,x∈![]() 的兩個根,
的兩個根,
由于該方程不存在兩個不等的根,
故不存在“4級理想區間”[m,n],
∴D結論錯誤
本題選擇D選項.


科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的右頂點為
的右頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,過點
,過點![]()
且斜率為![]() 的直線與
的直線與![]() 軸交于點
軸交于點![]() , 與橢圓交于另一個點
, 與橢圓交于另一個點![]() ,且點
,且點![]() 在
在![]() 軸上的射影恰好為點
軸上的射影恰好為點![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 且斜率大于
且斜率大于![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點(
兩點(![]() ),若
),若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x),當x,y∈R時,恒有f(x+y)=f(x)+f(y).當x>0時,f(x)>0
(1)求證:f(x)是奇函數;
(2)若![]() , 試求f(x)在區間[﹣2,6]上的最值;
, 試求f(x)在區間[﹣2,6]上的最值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,以坐標原點為極點, ![]() 軸的正半軸與極軸建立極坐標系,已知曲線
軸的正半軸與極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 且傾斜角為
且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從高一年級學生中隨機抽取40名中學生,將他們的期中考試數學成績(滿分100分,成績均為不低于40分的整數)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() ,得到如圖所示的頻率分布直方圖.
,得到如圖所示的頻率分布直方圖.
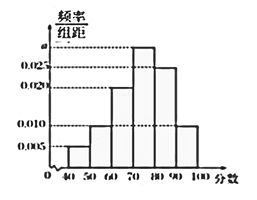
(1)求圖中實數![]() 的值;
的值;
(2)若該校高一年級共有640人,試估計該校高一年級期中考試數學成績不低于60分的人數;
(3)若從數學成績在![]() 與
與![]() 兩個分數段內的學生中隨機選取2名學生,求這2名學生的數學成績之差的絕對值不大于10的概率.
兩個分數段內的學生中隨機選取2名學生,求這2名學生的數學成績之差的絕對值不大于10的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與y軸的正半軸相交于點M,且橢圓E上相異兩點A、B滿足直線MA,MB的斜率之積為
與y軸的正半軸相交于點M,且橢圓E上相異兩點A、B滿足直線MA,MB的斜率之積為![]() .
.
(Ⅰ)證明直線AB恒過定點,并求定點的坐標;
(Ⅱ)求三角形ABM的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠擬造一座平面為長方形,面積為![]() 的三級污水處理池.由于地形限制,長、寬都不能超過
的三級污水處理池.由于地形限制,長、寬都不能超過![]() ,處理池的高度一定.如果池的四周墻壁的造價為
,處理池的高度一定.如果池的四周墻壁的造價為![]() 元
元![]() ,中間兩道隔墻的造價為
,中間兩道隔墻的造價為![]() 元
元![]() ,池底的造價為
,池底的造價為![]() 元
元![]() ,則水池的長、寬分別為多少米時,污水池的造價最低?最低造價為多少元?
,則水池的長、寬分別為多少米時,污水池的造價最低?最低造價為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com