
【題目】【2014福建,文22】已知函數![]() (
(![]() 為常數)的圖像與
為常數)的圖像與![]() 軸交于點
軸交于點![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() .
.
(1)求![]() 的值及函數
的值及函數![]() 的極值;
的極值;
(2)證明:當![]() 時,
時,![]()
(3)證明:對任意給定的正數![]() ,總存在
,總存在![]() ,使得當
,使得當![]() 時,恒有
時,恒有![]()
【答案】(1)當![]() 時,
時,![]() 有極小值
有極小值![]() ,
,![]() 無極大值.
無極大值.
(2)見解析.(3)見解析.
【解析】
試題分析:(1)由![]() ,得
,得![]() .
.
從而![]() .
.
令![]() ,得駐點
,得駐點![]() .討論可知:
.討論可知:
當![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
當![]() 時,
時,![]() 有極小值
有極小值![]() ,
,![]() 無極大值.
無極大值.
(2)令![]() ,則
,則![]() .
.
根據![]() ,知
,知![]() 在R上單調遞增,又
在R上單調遞增,又![]() ,
,
當![]() 時,由
時,由![]() ,即得.
,即得.
(3)思路一:對任意給定的正數c,取![]() ,
,
根據![]() .得到當
.得到當![]() 時,
時,![]() .
.
思路二:令![]() ,轉化得到只需
,轉化得到只需![]() 成立.
成立.
分![]() ,
,![]() ,應用導數研究
,應用導數研究![]() 的單調性.
的單調性.
思路三:就①![]() ,②
,②![]() ,加以討論.
,加以討論.
試題解析:
【解法一】
(1)由![]() ,得
,得![]() .
.
又![]() ,得
,得![]() .
.
所以![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
所以當![]() 時,
時,![]() 有極小值,
有極小值,
且極小值為![]() ,
,
![]() 無極大值.
無極大值.
(2)令![]() ,則
,則![]() .
.
由(1)得,![]() ,即
,即![]() .
.
所以![]() 在R上單調遞增,又
在R上單調遞增,又![]() ,
,
所以當![]() 時,
時,![]() ,即
,即![]() .
.
(3)對任意給定的正數c,取![]() ,
,
由(2)知,當![]() 時,
時,![]() .
.
所以當![]() 時,
時,![]() ,即
,即![]() .
.
因此,對任意給定的正數c,總存在![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.
【解法二】
(1)同解法一.
(2)同解法一.
(3)令![]() ,要使不等式
,要使不等式![]() 成立,只要
成立,只要![]() 成立.
成立.
而要使![]() 成立,則只需
成立,則只需![]() ,即
,即![]() 成立.
成立.
①若![]() ,則
,則![]() ,易知當
,易知當![]() 時,
時,![]() 成立.
成立.
即對任意![]() ,取
,取![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.
②若![]() ,令
,令![]() ,則
,則![]() ,
,
所以當![]() 時,
時,![]() ,
,![]() 在
在![]() 內單調遞增.
內單調遞增.
取![]() ,
,
![]() ,
,
易知![]() ,
,![]() ,所以
,所以![]() .
.
因此對任意![]() ,取
,取![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.
綜上,對任意給定的正數c,總存在![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.
【解法三】
(1)同解法一.
(2)同解法一.
(3)①若![]() ,取
,取![]() ,
,
由(2)的證明過程知,![]() ,
,
所以當![]() 時,有
時,有![]() ,即
,即![]() .
.
②若![]() ,
,
令![]() ,則
,則![]() ,
,
令![]() 得
得![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
取![]() ,
,
![]() ,
,
易知![]() ,又
,又![]() 在
在![]() 內單調遞增,
內單調遞增,
所以當![]() 時,恒有
時,恒有![]() ,即
,即![]() .
.
綜上,對任意給定的正數c,總存在![]() ,當
,當![]() 時,恒有
時,恒有![]() .
.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:
【題目】據市場分析,南雄市精細化工園某公司生產一種化工產品,當月產量在10噸至25噸時,月生產總成本y(萬元)可以看成月產量x(噸)的二次函數;當月產量為10噸時,月總成本為20萬元;當月產量為15噸時,月總成本最低為17.5萬元,為二次函數的頂點.寫出月總成本y(萬元)關于月產量x(噸)的函數關系.已知該產品銷售價為每噸1.6萬元,那么月產量為多少時,可獲最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 中點,
中點,![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,沿
,沿![]() 將四邊形
將四邊形![]() 折起,連接
折起,連接![]() .
.
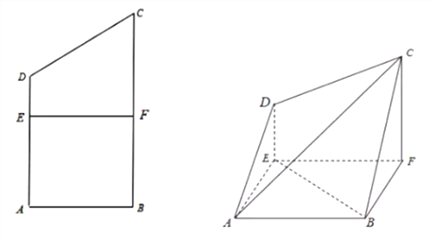
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() .
.
(I)求二面角![]() 的平面角的大小;
的平面角的大小;
(II)線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】制定投資計劃時,不僅要考慮可能獲得的盈利,而且要考慮可能出現的虧損.某投資人打算投資甲、乙兩個項目.根據預測,甲、乙項目可能的最大盈利率分別為100%和50%,可能的最大虧損分別為30%和10%.投資人計劃投資金額不超過10萬元,要求確保可能的資金虧損不超過1.8萬元.問投資人對甲、乙兩個項目各投資多少萬元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·哈爾濱高二檢測)如圖,下列四個幾何體中,它們的三視圖(正視圖、俯視圖、側視圖)有且僅有兩個相同,而另一個不同的兩個幾何體是________.


(1)棱長為2的正方體 (2)底面直徑和高均為2的圓柱

(3)底面直徑和高
均為2的圓錐
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2015高考四川,文21】已知函數f(x)=-2lnx+x2-2ax+a2,其中a>0.
(Ⅰ)設g(x)為f(x)的導函數,討論g(x)的單調性;
(Ⅱ)證明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在區間(1,+∞)內有唯一解.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
設橢圓![]() 的離心率為
的離心率為![]() ,其左焦點
,其左焦點![]() 與拋物線
與拋物線![]() 的焦點相同.
的焦點相同.
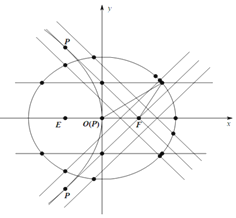
(1)求此橢圓的方程;
(2)若過此橢圓的右焦點![]() 的直線
的直線![]() 與曲線
與曲線![]() 只有一個交點
只有一個交點![]() ,則
,則
①求直線![]() 的方程;
的方程;
②橢圓上是否存在點![]() ,使得
,使得![]() ,若存在,請說明一共有幾個點;若不存在,請說明理由.
,若存在,請說明一共有幾個點;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,若普通6座以下私家車投保交強險第一年的費用(基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就是越高,具體浮動情況如下表:
元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就是越高,具體浮動情況如下表:
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發生有責任道路交通事故 | 下浮10% |
| 上兩個年度未發生有責任道路交通事故 | 下浮20% |
| 上三個及以上年度未發生有責任道路交通事故 | 下浮30% |
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 | 0% |
| 上一個年度發生兩次及兩次以上有責任道路交通事故 | 上浮10% |
| 上一個年度發生有責任道路交通死亡事故 | 上浮30% |
某機構為了 某一品牌普通6座以下私家車的投保情況,隨機抽取了60輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
類型 |
|
|
|
|
|
|
數量 | 10 | 5 | 5 | 20 | 15 | 5 |
以這60輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(1)按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定, ![]() ,記
,記![]() 為某同學家的一輛該品牌車在第四年續保時的費用,求
為某同學家的一輛該品牌車在第四年續保時的費用,求![]() 的分布列與數學期望;(數學期望值保留到個位數字)
的分布列與數學期望;(數學期望值保留到個位數字)
(2)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車,假設購進一輛事故車虧損5000元,一輛非事故車盈利10000元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至多有一輛事故車的概率;
②若該銷售商一次購進100輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年1月1日,作為貴陽市打造“千園之城”27個示范性公園之一的泉湖公園正式開園.元旦期間,為了活躍氣氛,主辦方設置了水上挑戰項目向全體市民開放.現從到公園游覽的市民中隨機抽取了60名男生和40名女生共100人進行調查,統計出100名市民中愿意接受挑戰和不愿意接受挑戰的男女生比例情況,具體數據如圖表:
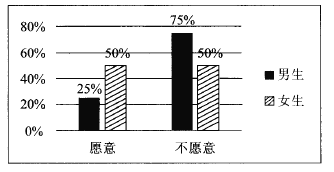
(1)根據條件完成下列![]()
列聯表,并判斷是否在犯錯誤的概率不超過1%的情況下愿意接受挑戰與性別有關?
愿意 | 不愿意 | 總計 | |
男生 | |||
女生 | |||
總計 |
(2)水上挑戰項目共有兩關,主辦方規定:挑戰過程依次進行,每一關都有兩次機會挑戰,通過第一關后才有資格參與第二關的挑戰,若甲參加每一關的每一次挑戰通過的概率均為![]()
,記甲通過的關數為![]()
,求![]()
的分布列和數學期望.
參考公式與數據:
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
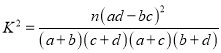
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com