【題目】已知0＜k＜4直線L：kx﹣2y﹣2k+8=0和直線M：2x+k2y﹣4k2﹣4=0與兩坐標軸圍成一個四邊形，則這個四邊形面積最小值時k值為（ ）
A.2
B.
C.
D.
【答案】D
【解析】解：如圖所示：
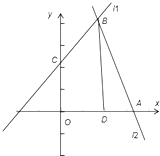
直線L：kx﹣2y﹣2k+8=0 即k（x﹣2）﹣2y+8=0，過定點B（2，4），
與y 軸的交點C（0，4﹣k），
直線M：2x+k2y﹣4k2﹣4=0，即 2x+k2 （y﹣4）﹣4=0，
過定點（2，4 ），與x 軸的交點A（2 k2+2，0），
由題意，四邊形的面積等于三角形ABD的面積和梯形 OCBD的面積之和，
∴所求四邊形的面積為 
×4×（2 k2+2﹣2）+ ×（4﹣k+4）×2=4k2﹣k+8，
∴當k= 
時，所求四邊形的面積最小，
故選： ．
【考點精析】利用一般式方程對題目進行判斷即可得到答案，需要熟知直線的一般式方程：關于
的二元一次方程
（A，B不同時為0）．
科目：高中數學 來源： 題型：
【題目】下列命題中正確的有 ．
①常數數列既是等差數列也是等比數列；
②在△ABC中，若sin2A+sin2B=sin2C，則△ABC為直角三角形；
③若A，B為銳角三角形的兩個內角，則tanAtanB＞1；
④若Sn為數列{an}的前n項和，則此數列的通項an=Sn﹣Sn﹣1（n＞1）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數φ（x）=a2x﹣ax（a＞0，a≠1）．
（1）求函數φ（x）在[﹣2，2]上的最大值；
（2）當a= 
時，φ（x）≤t2﹣2mt+2對所有的x∈[﹣2，2]及m∈[﹣1，1]恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知P為△ABC所在平面外一點，PA⊥PB，PB⊥PC，PC⊥PA，PH⊥平面 ABC，H，則H為△ABC的（ ）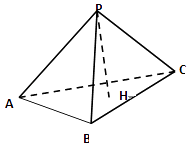 
A.重心
B.垂心
C.外心
D.內心
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C1： 
（a＞b＞0）的一個頂點與拋物線C2：x2=4y的焦點重合，F1、F2分別是橢圓C1的左、右焦點，C1的離心率e= 
，過F2的直線l與橢圓C1交于M，N兩點，與拋物線C2交于P，Q兩點．
（1）求橢圓C1的方程；
（2）當直線l的斜率k=﹣1時，求△PQF1的面積；
（3）在x軸上是否存在點A， 
為常數？若存在，求出點A的坐標和這個常數；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐P﹣ABCD中，底面ABCD是正方形，側棱PD⊥底面ABCD，PD=DC，E是PC的中點，過E點做EF⊥PB交PB于點F．求證： 
（1）PA∥平面DEB；
（2）PB⊥平面DEF．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2016年9月，第22屆魯臺經貿洽談會在濰坊魯臺會展中心舉行，在會展期間某展銷商銷售一種商品，根據市場調查，每件商品售價x（元）與銷量t（萬元）之間的函數關系如圖所示，又知供貨價格與銷量呈反比，比例系數為20．（注：每件產品利潤=售價﹣供貨價格） 
（1）求售價15元時的銷量及此時的供貨價格；
（2）當銷售價格為多少時總利潤最大，并求出最大利潤．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】四邊形ABCD是正方形，△PAB與△PAD均是以A為直角頂點的等腰直角三角形，點F是PB的中點，點E是邊BC上的任意一點． 
（1）求證：AF⊥EF；
（2）求二面角A﹣PC﹣B的平面角．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
