Question

10．點P是焦點為F₁，F₂的雙曲線$\frac{x^2}{25}-\frac{y^2}{16}=1$上的動點，若點I滿足 $\overrightarrow{PI}|{\overrightarrow{{F_1}{F_2}}}|+\overrightarrow{{F_1}I}|{\overrightarrow{P{F_2}}}|+\overrightarrow{{F_2}I}|{\overrightarrow{P{F_1}}}|=\overrightarrow 0$，則點I的橫坐標為±5．

Answer 1

分析 由題意可知I為焦點三角形PF₁F₂的內心，根據雙曲線的定義，及三角形內切圓的性質，即可求得丨丨AF₁丨-丨AF₂丨丨=2a=10，A是雙曲線與x軸的交點，即A₁，A₂，由IA⊥F₁F₂，則點I的橫坐標為±5．

解答 解：由點I滿足 $\overrightarrow{PI}|{\overrightarrow{{F_1}{F_2}}}|+\overrightarrow{{F_1}I}|{\overrightarrow{P{F_2}}}|+\overrightarrow{{F_2}I}|{\overrightarrow{P{F_1}}}|=\overrightarrow 0$，則I為焦點三角形PF₁F₂的內心，
設雙曲線雙曲線$\frac{x^2}{25}-\frac{y^2}{16}=1$的焦點三角形的內切圓且三邊F₁F₂，PF₁，PF₂于點A，B，C，雙曲線的兩個頂點為A₁，A₂，
則 丨PC丨=丨PB丨，丨F₁C丨=丨F₁A丨，丨F₂B丨=丨F₂A丨，
丨丨PF₁丨-丨PF₂丨丨=丨丨CF₁丨-丨BF₂丨丨=丨丨AF₁丨-丨AF₂丨丨，
由丨丨PF₁丨-丨PF₂丨丨=2a=10，丨丨AF₁丨-丨AF₂丨丨=2a=10，
∴A在雙曲線上，由A在F₁F₂上，
∴A是雙曲線與x軸的交點，即A₁，A₂，
由IA_i⊥F₁F₂，i=1，2，則
∴點I的橫坐標為±5，
故答案為：±5．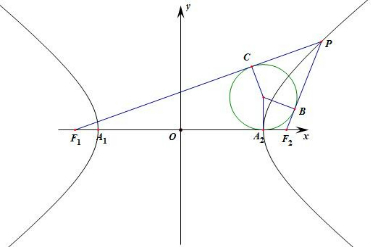

點評 本題考查雙曲線的定義，雙曲線焦點三角形內切圓的性質，雙曲線上任一支上一點與兩焦點組成的三角形的內心在實軸的射影為對應支的頂點結論的應用，考查數形結合思想，屬于中檔題．