【題目】某校在高二年級開設(shè)選修課，其中數(shù)學(xué)選修課開了三個班．選課結(jié)束后，有四名選修英語的同學(xué)要求改修數(shù)學(xué)，但數(shù)學(xué)選修每班至多可再接收兩名同學(xué)，那么安排好這四名同學(xué)的方案有（ ）
A.72種
B.54種
C.36種
D.18種
【答案】B
【解析】解：由題意知有四名選修英語的同學(xué)要求改修數(shù)學(xué)， 但數(shù)學(xué)選修每班至多可再接收兩名同學(xué)，需要分類來解，
將四名同學(xué)分成三組：1，1，2；和2，2兩種情況
分成1，1，2安排在三個數(shù)學(xué)班中：有 
=36；
分成兩組2，2．安排在兩個班里，有 
=18．
∴一共有36+18=54種安排方案
故選B．
由題意知，安排四名同學(xué)到三個班里，每班至多可再接收兩名同學(xué)，需要分類來解，將四名同學(xué)分成三組：1，1，2；和2，2兩種情況，首先要分組，再把分好的組排列到三個班里．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某地西紅柿從 
月 
日起開始上市．通過市場調(diào)查，得到西紅柿種植成本 
(就是每 
公斤西紅柿的種植成本，單位：元)與上市時間 
(單位：天)的數(shù)據(jù)如下表：
上市時間 | 50 | 110 | 250 |
種植成本 | 150 | 108 | 150 |
（1）根據(jù)上表數(shù)據(jù)，從下列函數(shù)中選取一個函數(shù)描述西紅柿種植成本與上市時間 的變化關(guān)系： 
； 
； 
； 
，并求出函數(shù)解析式；
（2）利用你選取的函數(shù)，求西紅柿種植成本最低時的上市天數(shù)及最低種植成本．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知等差數(shù)列{an}的首項a1=1，前n項和為Sn ， 且S1 ， 
成等差數(shù)列．
（1）求數(shù)列{an}的通項公式；
（2）若數(shù)列{bn}為遞增的等比數(shù)列，且集合{b1 ， b2 ， b3}{a1 ， a2 ， a3 ， a4 ， a5}，設(shè)數(shù)列{anbn}的前n項和為Tn ， 求Tn ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓C： 
+ 
=1（a＞b＞0）的左右焦點分別為F1 ， F2 ， 拋物線y2=4x與橢圓C有相同的焦點，且橢圓C過點 
． （I）求橢圓C的標準方程；
（Ⅱ）若橢圓C的右頂點為A，直線l交橢圓C于E、F兩點（E、F與A點不重合），且滿足AE⊥AF，若點P為EF中點，求直線AP斜率的最大值．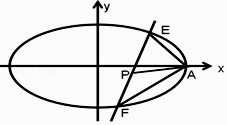
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】直三棱柱ABC﹣A1B1C1 中，AA1=AB=AC=1，E，F(xiàn)分別是CC1、BC 的中點，AE⊥ A1B1 ， D為棱A1B1上的點．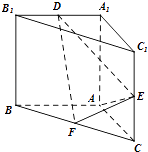
（1）證明：DF⊥AE；
（2）是否存在一點D，使得平面DEF與平面ABC所成銳二面角的余弦值為 
？若存在，說明點D的位置，若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
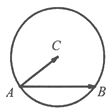
【題目】如圖，定圓C半徑為2，A為圓C上的一個定點，B為圓C上的動點，若點A，B，C不共線，且| 
| 
|對任意t∈（0，+∞）恒成立，則 
= ． 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖是用模擬方法估計圓周率π的程序框圖，P表示估計結(jié)果，則圖中空白框內(nèi)應(yīng)填入（ ） 
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)向量 
=（sinx，﹣1）， 
=（ 
cosx，﹣ 
），函數(shù)f（x）=（ + ） ．
（1）求函數(shù)f（x）的單調(diào)遞增區(qū)間；
（2）當x∈（0， 
）時，求函數(shù)f（x）的值域．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在銳角△ABC中，角A，B，C的對邊分別為a，b，c，滿足 
= 
．
（1）求角A的大小；
（2）若a= 
，△ABC的面積S△ABC=3 
，求b+c的值，；
（3）若函數(shù)f（x）=2sinxcos（x+ 
），求f（B）的取值范圍．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com