
【題目】設函數f(x)=eax+λlnx,其中a<0,0<λ< ![]() ,e是自然對數的底數
,e是自然對數的底數
(1)求證:函數f(x)有兩個極值點;
(2)若﹣e≤a<0,求證:函數f(x)有唯一零點.
【答案】
(1)證明: f′(x)=aeax+ ![]() =
= ![]() ,(x>0),
,(x>0),
令g(x)=axeax+λ,其中a<0,x>0,
求導得:g′(x)=aeax(1+ax),
令g′(x)=0,解得:x=﹣ ![]() ,
,
x∈(0,﹣ ![]() )時,g′(x)<0,g(x)遞減,
)時,g′(x)<0,g(x)遞減,
x∈(﹣ ![]() ,+∞)時,g′(x)>0,g(x)遞增,
,+∞)時,g′(x)>0,g(x)遞增,
x=﹣ ![]() 時,g(x)取得極小值,也是最小值g(﹣
時,g(x)取得極小值,也是最小值g(﹣ ![]() )=λ﹣
)=λ﹣ ![]() ,
,
∵0<λ< ![]() ,∴g(﹣
,∴g(﹣ ![]() )=λ﹣
)=λ﹣ ![]() <0,又g(0)=λ>0,
<0,又g(0)=λ>0,
∴g(﹣ ![]() )g(0)<0,
)g(0)<0,
∴函數f(x)有兩個極值點;
(2)證明:由(1)得:
不妨令x2∈(﹣ ![]() ,+∞),
,+∞),
故ax2 ![]() +λ=0,
+λ=0,
故f(x2)=(1﹣ax2lnx2) ![]() ,
,
令h(x)=1﹣axlnx,x∈(﹣ ![]() ,+∞),
,+∞),
h′(x)=﹣a(lnx+1)>﹣a(ln ![]() +1)=0,
+1)=0,
∴f(x2)>0,∵f(0)→負數,
∴函數f(x)有唯一零點.
【解析】(1)求出函數的導數,解關于導函數的不等式,求出函數的單調區間,從而判斷函數的極值點的個數;(2)根據函數的單調性,令x2∈(﹣ ![]() ,+∞),故f(x2)=(1﹣ax2lnx2)
,+∞),故f(x2)=(1﹣ax2lnx2) ![]() ,令h(x)=1﹣axlnx,x∈(﹣
,令h(x)=1﹣axlnx,x∈(﹣ ![]() ,+∞),根據函數的單調性判斷即可.
,+∞),根據函數的單調性判斷即可.
【考點精析】本題主要考查了函數的極值與導數的相關知識點,需要掌握求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值才能正確解答此題.
是極小值才能正確解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
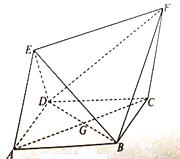
【題目】如圖,四邊形 ![]() 為菱形,四邊形
為菱形,四邊形 ![]() 為平行四邊形,設
為平行四邊形,設 ![]() 與
與 ![]() 相交于點
相交于點 ![]() ,
, ![]() .
.
(1)證明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() 與平面
與平面 ![]() 所成角為60°,求二面角
所成角為60°,求二面角 ![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系的原點為極點,以x軸的正半軸為極軸建立極坐標系.設曲線C的參數方程為 ![]() (α是參數),直線l的極坐標方程為ρcos(θ+
(α是參數),直線l的極坐標方程為ρcos(θ+ ![]() )=2
)=2 ![]() .
.
(1)求直線l的直角坐標方程和曲線C的普通方程;
(2)設點P為曲線C上任意一點,求點P到直線l的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們國家正處于老齡化社會中,老有所依也是政府的民生工程.某市共有戶籍人口400萬,其中老人(年齡60歲及以上)人數約有66萬,為了了解老人們的健康狀況,政府從老人中隨機抽取600人并委托醫療機構免費為他們進行健康評估,健康狀況共分為不能自理、不健康尚能自理、基本健康、健康四個等級,并以80歲為界限分成兩個群體進行統計,樣本分布被制作成如圖表: 
(1)若采用分層抽樣的方法再從樣本中的不能自理的老人中抽取8人進一步了解他們的生活狀況,則兩個群體中各應抽取多少人?
(2)估算該市80歲及以上長者占全市戶籍人口的百分比;
(3)據統計該市大約有五分之一的戶籍老人無固定收入,政府計劃為這部分老人每月發放生活補貼,標準如下: ①80歲及以上長者每人每月發放生活補貼200元;
②80歲以下老人每人每月發放生活補貼120元;
③不能自理的老人每人每月額外發放生活補貼100元.試估計政府執行此計劃的年度預算.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為2的正方體ABCD﹣A1B1C1D1中,E為對角線B1D上的一點,M,N為對角線AC上的兩個動點,且線段MN的長度為1. 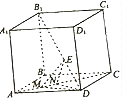
⑴當N為對角線AC的中點且DE= ![]() 時,則三棱錐E﹣DMN的體積是;
時,則三棱錐E﹣DMN的體積是;
⑵當三棱錐E﹣DMN的體積為 ![]() 時,則DE= .
時,則DE= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 的最小正周期為4π,則( )
的最小正周期為4π,則( )
A.函數f(x)的圖象關于原點對稱
B.函數f(x)的圖象關于直線 ![]() 對稱
對稱
C.函數f(x)圖象上的所有點向右平移 ![]() 個單位長度后,所得的圖象關于原點對稱
個單位長度后,所得的圖象關于原點對稱
D.函數f(x)在區間(0,π)上單調遞增
查看答案和解析>>
科目:高中數學 來源: 題型:
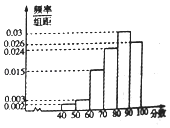
【題目】2017年3月14日,“ofo共享單車”終于來到蕪湖,ofo共享單車又被親切稱作“小黃車”是全球第一個無樁共享單車平臺,開創了首個“單車共享”模式.相關部門準備對該項目進行考核,考核的硬性指標是:市民對該項目的滿意指數不低于0.8,否則該項目需進行整改,該部門為了了解市民對該項目的滿意程度,隨機訪問了使用共享單車的100名市民,并根據這100名市民對該項目滿意程度的評分,繪制了如下頻率分布直方圖: (I)為了了解部分市民對“共享單車”評分較低的原因,該部門從評分低于60分的市民中隨機抽取2人進行座談,求這2人評分恰好都在[50,60)的概率;
(II)根據你所學的統計知識,判斷該項目能否通過考核,并說明理由.
(注:滿意指數= ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A,B,C的對邊分別為a,b,c,且滿足cos2B﹣cos2C﹣sin2A=sinAsinB.
(1)求角C;
(2)若c=2 ![]() ,△ABC的中線CD=2,求△ABC面積S的值.
,△ABC的中線CD=2,求△ABC面積S的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com