
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)設函數![]() ,函數
,函數![]() 有且僅有一個零點.
有且僅有一個零點.
(i)求![]() 的值;
的值;
(ii)若![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)(ⅰ)a=1(ⅱ)
(2)(ⅰ)a=1(ⅱ)![]()
【解析】試題分析:(1)當a=﹣1時,函數f(x)=(x2﹣2x)lnx+ax2+2=(x2﹣2x)lnx﹣x2+2,求出f′(x),則k=f′(1),代入直線方程的點斜式可得切線的方程.
(2)①令g(x)=f(x)﹣x﹣2=0,則(x2﹣2x)lnx+ax2+2=x+2,即![]() ,構造函數h(x)=
,構造函數h(x)=![]() ,確定h(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減,可得h(x)max=h(1)=1,即可求a的值;
,確定h(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減,可得h(x)max=h(1)=1,即可求a的值;
②當a=1時,g(x)=(x2﹣2x)lnx+x2﹣x,若![]() ,g(x)≥m,只需g(x)min≥m.
,g(x)≥m,只需g(x)min≥m.
試題解析:
(1)當![]() 時,
時, ![]() ,
, ![]() ,
,
∴![]()
![]() ,又
,又![]()
∴![]() 在
在![]() 處的切線方程
處的切線方程![]() .
.
(2)(ⅰ)令![]() ,則
,則![]()
∴![]() 令
令![]() , 則
, 則![]() .
.
令![]() ,則
,則![]()
![]() ,
,
![]() ,
,![]() 在
在![]() 上是減函數 又
上是減函數 又![]() ,
,
∴當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
![]() ,∴當函數
,∴當函數![]() 有且只有一個零點時,
有且只有一個零點時, ![]() .
.
(ⅱ)當![]() ,
, ![]() ,若
,若![]() 時,
時, ![]() 恒成立,
恒成立,
只需![]()
![]() .令
.令![]() 得
得![]() 或
或![]() ,
,
![]() ,
, ![]() 函數
函數![]() 在
在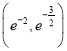 上單調遞增,在
上單調遞增,在 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
又∵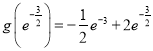 ,
, ![]()
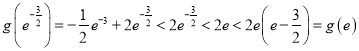 ,即
,即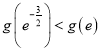 .
.
∴![]() ,
, ![]() .
.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】某單位200名職工的年齡分布情況如圖,現要從中抽取40名職工作樣本.用系統抽樣法,將全體職工隨機按1~200編號,并按編號順序平均分為40組(1~5號,6~10號,…,196~200號).若第5組抽出的號碼為22,則第8組抽出的號碼應是________.若用分層抽樣法,則40歲的以下的年齡段應抽取__________人.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),將曲線
為參數),將曲線![]() 上各點的橫坐標都縮短為原來的
上各點的橫坐標都縮短為原來的![]() 倍,縱坐標坐標都伸長為原來的
倍,縱坐標坐標都伸長為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,在極坐標系(與直角坐標系
,在極坐標系(與直角坐標系![]() 取相同的單位長度,且以原點
取相同的單位長度,且以原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸)中,直線
軸非負半軸為極軸)中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為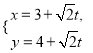 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系
軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系![]() 有相同的長度單位,曲線
有相同的長度單位,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() 點的坐標為
點的坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的是( )
A. 設隨機變量![]() ,則
,則![]()
B. 線性回歸直線不一定過樣本中心點![]()
C. 若兩個隨機變量的線性相關性越強,則相關系數![]() 的值越接近于1
的值越接近于1
D. 先把高三年級的2000名學生編號:1到2000,再從編號為1到50的50名學生中隨機抽取1名學生,其編號為![]() ,然后抽取編號為
,然后抽取編號為![]() ,
, ![]() ,
, ![]() ,……的學生,這樣的抽樣方法是分層抽樣
,……的學生,這樣的抽樣方法是分層抽樣
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區某農產品近幾年的產量統計如下表:

(1)根據表中數據,建立![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若近幾年該農產品每千克的價格![]() (單位:元)與年產量
(單位:元)與年產量![]() 滿足的函數關系式為
滿足的函數關系式為![]() ,且每年該農產品都能售完.
,且每年該農產品都能售完.
①根據(1)中所建立的回歸方程預測該地區![]() 年該農產品的產量;
年該農產品的產量;
②當![]() 為何值時,銷售額
為何值時,銷售額![]() 最大?
最大?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: 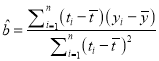 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場為了了解顧客的購物信息,隨機在商場收集了![]() 位顧客購物的相關數據如下表:
位顧客購物的相關數據如下表:
一次購物款(單位:元) |
|
|
|
|
|
顧客人數 |
|
|
|
|
|
統計結果顯示![]() 位顧客中購物款不低于
位顧客中購物款不低于![]() 元的顧客占
元的顧客占![]() ,該商場每日大約有
,該商場每日大約有![]() 名顧客,為了增加商場銷售額度,對一次購物不低于
名顧客,為了增加商場銷售額度,對一次購物不低于![]() 元的顧客發放紀念品.
元的顧客發放紀念品.
(Ⅰ)試確定![]() ,
, ![]() 的值,并估計每日應準備紀念品的數量;
的值,并估計每日應準備紀念品的數量;
(Ⅱ)現有![]() 人前去該商場購物,求獲得紀念品的數量
人前去該商場購物,求獲得紀念品的數量![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家電公司根據銷售區域將銷售員分成![]() 兩組.2017年年初,公司根據銷售員的銷售業績分發年終獎,銷售員的銷售額(單位:十萬元)在區間
兩組.2017年年初,公司根據銷售員的銷售業績分發年終獎,銷售員的銷售額(單位:十萬元)在區間![]() 內對應的年終獎分別為2萬元,2.5萬元,3萬元,3.5萬元.已知200名銷售員的年銷售額都在區間
內對應的年終獎分別為2萬元,2.5萬元,3萬元,3.5萬元.已知200名銷售員的年銷售額都在區間![]() 內,將這些數據分成4組:
內,將這些數據分成4組: ![]() ,得到如下兩個頻率分布直方圖:
,得到如下兩個頻率分布直方圖:

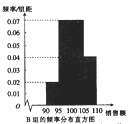
以上面數據的頻率作為概率,分別從![]() 組與
組與![]() 組的銷售員中隨機選取1位,記
組的銷售員中隨機選取1位,記![]() 分別表示
分別表示![]() 組與
組與![]() 組被選取的銷售員獲得的年終獎.
組被選取的銷售員獲得的年終獎.
(1)求![]() 的分布列及數學期;
的分布列及數學期;
(2)試問![]() 組與
組與![]() 組哪個組銷售員獲得的年終獎的平均值更高?為什么?
組哪個組銷售員獲得的年終獎的平均值更高?為什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018河南豫南九校高三下學期第一次聯考】設函數![]() .
.
(I)當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的范圍;
的范圍;
(II)若![]() 在
在![]() 處的切線為
處的切線為![]() ,且方程
,且方程![]() 恰有兩解,求實數
恰有兩解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com