
已知函數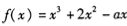 .對于任意實數x恒有
.對于任意實數x恒有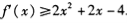
(1)求實數 的最大值;
的最大值;
(2)當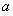 最大時,函數
最大時,函數 有三個零點,求實數k的取值范圍。
有三個零點,求實數k的取值范圍。
(1)3;(2)
【解析】
試題分析:(1)根據函數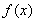 求出導函數,再根據所給的不等式,利用恒成立的條件求出實數
求出導函數,再根據所給的不等式,利用恒成立的條件求出實數 的范圍,從而確定
的范圍,從而確定 的最大值.
的最大值.
(2)由(1)可得 的值,從而根據函數
的值,從而根據函數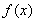 確定函數
確定函數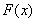 的解析式,由于函數
的解析式,由于函數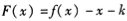 有三個零點,所以通過對函數
有三個零點,所以通過對函數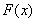 求導,了解函數
求導,了解函數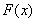 的圖像的走向,以及對函數的極值的正負性作出規定,即可得到所需的結論.
的圖像的走向,以及對函數的極值的正負性作出規定,即可得到所需的結論.
試題解析:(1)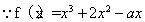
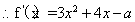 對于
對于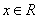 恒有
恒有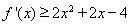 ,即
,即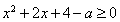 對于
對于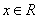 恒成立
恒成立
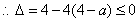
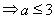
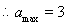
(2) 有三個零點
有三個零點
 有三個不同的實根
有三個不同的實根 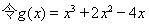 ,則
,則
令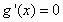 解得
解得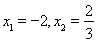
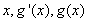 情況如下表:
情況如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 單調遞增 | 極大值8 | 單調遞減 | 極小極 | 單調遞增 |
由上表知,當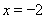 時
時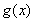 取得極大值
取得極大值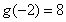 ,當
,當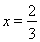 時
時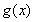 取得極小值
取得極小值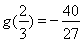
數形結合可知,實數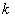 的取值范圍為
的取值范圍為 .
.
考點:1.函數的導數.2.函數的最值.3.函數的極值.4.函數與方程的關系.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南大學出版社系列答案
同步練習西南大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:
| 3 |
| 1 |
| 2 |
| 5π |
| 12 |
| 3 |
| π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:荊門市2008屆高三數學試題(理)模擬訓練題 題型:022
有如下四個命題:
①已知函數![]() (b為實常數,e是自然對數的底數),若f(x)在區間[1,+∞)內為減函數,則b的取值范圍是(0,+∞).
(b為實常數,e是自然對數的底數),若f(x)在區間[1,+∞)內為減函數,則b的取值范圍是(0,+∞).
②已知點A(x1,y1),B(x2,y2)是函數y=sinx(-π<x<0)圖象上的兩個不同點,則一定有![]() ;
;
③已知f(x)是定義在R上的不恒為零的函數,且對于任意的a,b∈R,滿足:f(ab)=af(b)+bf(a),f(2)=2,an=![]() (n∈N*),則數列{an}一定為等差數列
(n∈N*),則數列{an}一定為等差數列
④已知O是△ABC所在平面上一定點,動點P滿足: .則P點的軌跡一定通過△ABC的重心其中正確命題的序號為________
.則P點的軌跡一定通過△ABC的重心其中正確命題的序號為________
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
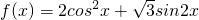 ,
,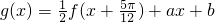 ,其中a,b為非零實常數.
,其中a,b為非零實常數.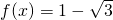 ,
,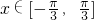 ,求x;
,求x;查看答案和解析>>
科目:高中數學 來源: 題型:
若函數![]() 對于定義域中的任意實數
對于定義域中的任意實數![]() ,都存在實常數
,都存在實常數![]() 滿足
滿足
![]() ,則稱
,則稱![]() 關于點
關于點![]() 對稱.
對稱.
(1)已知函數![]()
![]() 的圖象關于
的圖象關于![]() 對稱,求實數
對稱,求實數![]() 的值;
的值;
(2)在(1)的結論下,已知![]() ,若對于任意的正實數
,若對于任意的正實數![]() 和負實數
和負實數![]() ,恒有
,恒有![]()
![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com