
【題目】函數(shù) ![]() 的最小正周期為π,若其圖象向左平移
的最小正周期為π,若其圖象向左平移 ![]() 個單位后得到的函數(shù)為奇函數(shù),則函數(shù)f(x)的圖象( )
個單位后得到的函數(shù)為奇函數(shù),則函數(shù)f(x)的圖象( )
A.關(guān)于點(diǎn) ![]() 對稱
對稱
B.關(guān)于點(diǎn) ![]() 對稱
對稱
C.關(guān)于直線 ![]() 對稱
對稱
D.關(guān)于直線 ![]() 對稱
對稱
【答案】C
【解析】解:由已知 ![]() ,則ω=2
,則ω=2
f(x)=sin(2x+φ)向左移 ![]() 個單位得
個單位得 ![]() 為奇函數(shù)
為奇函數(shù)
則有 ![]() ,
,
∵|φ|< ![]() ∴φ=
∴φ= ![]()
即 ![]() .代入選項檢驗,當(dāng)x=
.代入選項檢驗,當(dāng)x= ![]() 時,
時, ![]() 為函數(shù)的最大值
為函數(shù)的最大值
根據(jù)三角函數(shù)的性質(zhì)可知對稱軸處將取得函數(shù)的最值,C正確.
故選:C
【考點(diǎn)精析】本題主要考查了正弦函數(shù)的對稱性和函數(shù)y=Asin(ωx+φ)的圖象變換的相關(guān)知識點(diǎn),需要掌握正弦函數(shù)的對稱性:對稱中心![]() ;對稱軸
;對稱軸![]() ;圖象上所有點(diǎn)向左(右)平移
;圖象上所有點(diǎn)向左(右)平移![]() 個單位長度,得到函數(shù)
個單位長度,得到函數(shù)![]() 的圖象;再將函數(shù)
的圖象;再將函數(shù)![]() 的圖象上所有點(diǎn)的橫坐標(biāo)伸長(縮短)到原來的
的圖象上所有點(diǎn)的橫坐標(biāo)伸長(縮短)到原來的![]() 倍(縱坐標(biāo)不變),得到函數(shù)
倍(縱坐標(biāo)不變),得到函數(shù)![]() 的圖象;再將函數(shù)
的圖象;再將函數(shù)![]() 的圖象上所有點(diǎn)的縱坐標(biāo)伸長(縮短)到原來的
的圖象上所有點(diǎn)的縱坐標(biāo)伸長(縮短)到原來的![]() 倍(橫坐標(biāo)不變),得到函數(shù)
倍(橫坐標(biāo)不變),得到函數(shù)![]() 的圖象才能正確解答此題.
的圖象才能正確解答此題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,拋物線C1:x2=4y,C2:x2=-2py(p>0).點(diǎn)M(x0,y0)在拋物線C2上,過M作C1的切線,切點(diǎn)為A,B(M為原點(diǎn)O時,A,B重合于O).當(dāng)x0=1-![]() 時,切線MA的斜率為-
時,切線MA的斜率為-![]() .
.
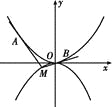
(1)求p的值;
(2)當(dāng)M在C2上運(yùn)動時,求線段AB中點(diǎn)N的軌跡方程(A,B重合于O時,中點(diǎn)為O).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從某校高三學(xué)生中隨機(jī)抽取了![]() 名學(xué)生,統(tǒng)計了期末數(shù)學(xué)考試成績?nèi)缦卤恚?/span>
名學(xué)生,統(tǒng)計了期末數(shù)學(xué)考試成績?nèi)缦卤恚?/span>
(1)請在頻率分布表中的①、②位置上填上相應(yīng)的數(shù)據(jù),并在給定的坐標(biāo)系中作出這些數(shù)據(jù)的頻率分布直方圖,再根據(jù)頻率分布直方圖估計這![]() 名學(xué)生的平均成績;
名學(xué)生的平均成績;
(2)用分層抽樣的方法在分?jǐn)?shù)在![]() 內(nèi)的學(xué)生中抽取一個容量為
內(nèi)的學(xué)生中抽取一個容量為![]() 的樣本,將該樣本看成一個總體,從中任取
的樣本,將該樣本看成一個總體,從中任取![]() 人,求至少有
人,求至少有![]() 人的分?jǐn)?shù)在
人的分?jǐn)?shù)在![]() 內(nèi)的概率.
內(nèi)的概率.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線經(jīng)過點(diǎn)M( ![]() ).
).
(1)如果此雙曲線的漸近線為 ![]() ,求雙曲線的標(biāo)準(zhǔn)方程;
,求雙曲線的標(biāo)準(zhǔn)方程;
(2)如果此雙曲線的離心率e=2,求雙曲線的標(biāo)準(zhǔn)方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點(diǎn),
的中點(diǎn), ![]() 在
在![]() 上,且
上,且![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)在線段上![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使二面角
,使二面角
![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某氣象站觀測點(diǎn)記錄的連續(xù)4天里, ![]() 指數(shù)
指數(shù)![]() 與當(dāng)天的空氣水平可見度
與當(dāng)天的空氣水平可見度![]() (單位
(單位![]() )的情況如下表1:
)的情況如下表1:
![]()
哈爾濱市某月![]() 指數(shù)頻數(shù)分布如下表2:
指數(shù)頻數(shù)分布如下表2:
![]()
(1)設(shè)![]() ,根據(jù)表1的數(shù)據(jù),求出
,根據(jù)表1的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(參考公式: ![]() ,其中
,其中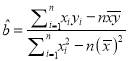 ,
, ![]() )
)
(2)小張開了一家洗車店,經(jīng)統(tǒng)計,當(dāng)![]() 不高于200時,洗車店平均每天虧損約2000元;當(dāng)
不高于200時,洗車店平均每天虧損約2000元;當(dāng)![]() 在
在![]() 時,洗車店平均每天收入約4000元;當(dāng)
時,洗車店平均每天收入約4000元;當(dāng)![]() 大于400時,洗車店平均每天收入約7000元;根據(jù)表2估計校長的洗車店該月份平均每天的收入.
大于400時,洗車店平均每天收入約7000元;根據(jù)表2估計校長的洗車店該月份平均每天的收入.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量 ![]() =(2cos2x,
=(2cos2x, ![]() ),
), ![]() =(1,sin2x),函數(shù)f(x)=
=(1,sin2x),函數(shù)f(x)= ![]()
![]() ﹣1.
﹣1.
(1)當(dāng)x= ![]() 時,求|a﹣b|的值;
時,求|a﹣b|的值;
(2)求函數(shù)f(x)的最小正周期以及單調(diào)遞增區(qū)間;
(3)求方程f(x)=k,(0<k<2),在[﹣ ![]() ,
, ![]() ]內(nèi)的所有實數(shù)根之和.
]內(nèi)的所有實數(shù)根之和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c且滿足csinA=acosC
(1)求角C的大小;
(2)求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A.有兩個面平行,其余各面都是四邊形的幾何體叫棱柱.
B.有兩個面平行,其余各面都是平行四邊形的幾何體叫棱柱.
C.有一個面是多邊形,其余各面都是三角形的幾何體叫棱錐.
D.棱臺各側(cè)棱的延長線交于一點(diǎn).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com