
【題目】![]() ,
,![]() 為空間中兩條互相垂直的直線,等腰直角三角形
為空間中兩條互相垂直的直線,等腰直角三角形![]() 的直角邊
的直角邊![]() 所在直線與
所在直線與![]() ,
,![]() 都垂直,斜邊
都垂直,斜邊![]() 以直線
以直線![]() 為旋轉軸旋轉,有下列結論:
為旋轉軸旋轉,有下列結論:
(1)當直線![]() 與
與![]() 成
成![]() 角時,
角時,![]() 與
與![]() 成
成![]() 角;
角;
(2)當直線![]() 與
與![]() 成
成![]() 角時,
角時,![]() 與
與![]() 成
成![]() 角;
角;
(3)直線![]() 與
與![]() 所成角的最小值為
所成角的最小值為![]() ;
;
(4)直線![]() 與
與![]() 所成角的最小值為
所成角的最小值為![]() ;
;
其中正確的是______(填寫所有正確結論的編號).
【答案】(1)(3)
【解析】
由題意知,a、b、AC三條直線兩兩相互垂直,構建如圖所示的邊長為1的正方體,|AC|=1,|AB|![]() ,斜邊AB以直線AC為旋轉軸,則A點保持不變,B點的運動軌跡是以C為圓心,1為半徑的圓,以C坐標原點,以CD為x軸,CB為y軸,CA為z軸,建立空間直角坐標系,利用向量法能求出結果.
,斜邊AB以直線AC為旋轉軸,則A點保持不變,B點的運動軌跡是以C為圓心,1為半徑的圓,以C坐標原點,以CD為x軸,CB為y軸,CA為z軸,建立空間直角坐標系,利用向量法能求出結果.
由題意知,a、b、AC三條直線兩兩相互垂直,畫出圖形如圖,

不妨設圖中所示正方體邊長為1,
故|AC|=1,|AB|![]() ,
,
斜邊AB以直線AC為旋轉軸,則A點保持不變,
B點的運動軌跡是以C為圓心,1為半徑的圓,
以C坐標原點,以CD為x軸,CB為y軸,CA為z軸,建立空間直角坐標系,
則D(1,0,0),A(0,0,1),直線a的方向單位向量![]() (0,1,0),|
(0,1,0),|![]() |=1,
|=1,
直線b的方向單位向量![]() (1,0,0),|
(1,0,0),|![]() |=1,
|=1,
設B點在運動過程中的坐標中的坐標B′(cosθ,sinθ,0),
其中θ為B′C與CD的夾角,θ∈[0,2π),
∴AB′在運動過程中的向量為![]() (cosθ,sinθ,﹣1),|
(cosθ,sinθ,﹣1),|![]() |
|![]() ,
,
設![]() 與
與![]() 所成夾角為α∈[0,
所成夾角為α∈[0,![]() ],
],
則cosα![]() |sinθ|∈[0,
|sinθ|∈[0,![]() ],
],
∴α∈[![]() ,
,![]() ],∴(3)正確,(4)錯誤.
],∴(3)正確,(4)錯誤.
設![]() 與
與![]() 所成夾角為β∈[0,
所成夾角為β∈[0,![]() ],
],
cosβ |cosθ|,
|cosθ|,
當![]() 與
與![]() 夾角為60°時,即α
夾角為60°時,即α![]() ,
,
|sinθ|![]() ,
,
∵cos2θ+sin2θ=1,∴cosβ![]() |cosθ|
|cosθ|![]() ,
,
∵β∈[0,![]() ],∴β
],∴β![]() ,此時
,此時![]() 與
與![]() 的夾角為60°,
的夾角為60°,
∴(1)正確,(2)錯誤.
故答案為:(1)(3).


科目:高中數學 來源: 題型:
【題目】某學校![]() 、
、![]() 兩個班的數學興趣小組在一次數學對抗賽中的成績繪制莖葉圖如下,通過莖葉圖比較兩班數學興趣小組成績的平均值及方差
兩個班的數學興趣小組在一次數學對抗賽中的成績繪制莖葉圖如下,通過莖葉圖比較兩班數學興趣小組成績的平均值及方差
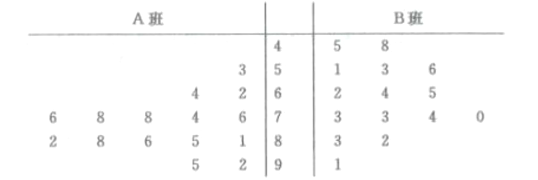
①![]() 班數學興趣小組的平均成績高于
班數學興趣小組的平均成績高于![]() 班的平均成績
班的平均成績
②![]() 班數學興趣小組的平均成績高于
班數學興趣小組的平均成績高于![]() 班的平均成績
班的平均成績
③![]() 班數學興趣小組成績的標準差大于
班數學興趣小組成績的標準差大于![]() 班成績的標準差
班成績的標準差
④![]() 班數學興趣小組成績的標準差大于
班數學興趣小組成績的標準差大于![]() 班成績的標準差
班成績的標準差
其中正確結論的編號為( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() ,且點
,且點![]() 到橢圓C的兩焦點的距離之和為
到橢圓C的兩焦點的距離之和為![]() .
.

(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ) 若![]() ,
,![]() 是橢圓
是橢圓![]() 上的兩個點,線段
上的兩個點,線段![]() 的中垂線
的中垂線![]() 的斜率為
的斜率為![]() ,且直線
,且直線![]() 與
與![]() 交于點
交于點![]() ,求證:點
,求證:點![]() 在直線
在直線![]() 上.
上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,底面
,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
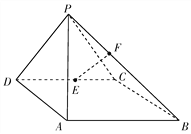
(Ⅰ)求證: ![]() ;
;
(Ⅱ)試確定點![]() 的位置,使得直線
的位置,使得直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:an+1-an=d(n∈N*),前n項和記為Sn,a1=4,S3=21.
(1)求數列{an}的通項公式;
(2)設數列{bn}滿足b1=![]() ,bn+1-bn=2an,求數列{bn}的通項公式.
,bn+1-bn=2an,求數列{bn}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,過點
中,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com