
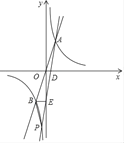
【題目】如圖,過原點O的直線與雙曲線y=![]() 交于上A(m,n)、B,過點A的直線交x軸正半軸于點D,交y軸負半軸于點E,交雙曲線y=
交于上A(m,n)、B,過點A的直線交x軸正半軸于點D,交y軸負半軸于點E,交雙曲線y=![]() 于點P.
于點P.
(1)當m=2時,求n的值;
(2)當OD:OE=1:2,且m=3時,求點P的坐標;
(3)若AD=DE,連接BE,BP,求△PBE的面積.
【答案】(1)3;(2)P(﹣2,﹣3);(3)3.
【解析】
(1)把A(2,n)代入解析式即可求出n;(2)先求出A點坐標,設OD=a,則OE=2a,得D(a,0),E(0,﹣2a),直線DE的解析式為y=2x﹣2a,把點A(3,2)代入求出a,再聯立兩函數即可求出交點P;(3)由AD=DE,點D在x軸坐標軸上,點E在y軸負半軸上,故A(m,n),E(0,﹣n),D(![]() m,0),求得直線DE的解析式為y=
m,0),求得直線DE的解析式為y=![]() x﹣n,又mn=6,得y=
x﹣n,又mn=6,得y=![]() x﹣n,與y=
x﹣n,與y=![]() 聯立得
聯立得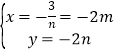 ,即為P點坐標,由直線AB的解析式為y=
,即為P點坐標,由直線AB的解析式為y=![]() x與雙曲線聯立解得B(﹣m,﹣n),再根據S△PBE=
x與雙曲線聯立解得B(﹣m,﹣n),再根據S△PBE=![]() BE×|yE﹣yP|=
BE×|yE﹣yP|=![]() ×m×|﹣n﹣(﹣2n)|求出等于3.
×m×|﹣n﹣(﹣2n)|求出等于3.
解:(1)∵點A(m,n)在雙曲線y=![]() 上,
上,
∴mn=6,
∵m=2,
∴n=3;
(2)由(1)知,mn=6,
∵m=3,
∴n=2,
∴A(3,2),
∵OD:OE=1:2,
設OD=a,則OE=2a,
∵點D在x軸坐標軸上,點E在y軸負半軸上,
∴D(a,0),E(0,﹣2a),
∴直線DE的解析式為y=2x﹣2a,
∵點A(3,2)在直線y=2x﹣2a上,
∴6﹣2a=2,
∴a=2,
∴直線DE的解析式為y=2x﹣4①,
∵雙曲線的解析式為y=![]() ②,
②,
聯立①②解得,![]() (點A的橫縱坐標,所以舍去)或
(點A的橫縱坐標,所以舍去)或![]() ,
,
∴P(﹣2,﹣3);
(3)∵AD=DE,點D在x軸坐標軸上,點E在y軸負半軸上,A(m,n),
∴E(0,﹣n),D(![]() m,0),
m,0),
∴直線DE的解析式為y=![]() x﹣n,
x﹣n,
∵mn=6,
∴m=![]() ,
,
∴y=![]() x﹣n③,
x﹣n③,
∵雙曲線的解析式為y=![]() ④,
④,
聯立③④解得,
∴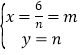 (點A的橫縱坐標,所以舍去)或
(點A的橫縱坐標,所以舍去)或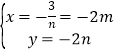 ,
,
∴P(﹣2m,﹣2n),
∵A(m,n),
∴直線AB的解析式為y=![]() x⑤.
x⑤.
聯立④⑤解得,![]() (點A的橫縱坐標,所以舍去)或
(點A的橫縱坐標,所以舍去)或![]()
∴B(﹣m,﹣n),
∵E(0,﹣n),
∴BE∥x軸,
∴S△PBE=![]() BE×|yE﹣yP|=
BE×|yE﹣yP|=![]() ×m×|﹣n﹣(﹣2n)|=
×m×|﹣n﹣(﹣2n)|=![]() mn=3.
mn=3.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】2018年首屆“進博會”期間,上海對周邊道路進行限速行駛.道路![]() 段為監測區,
段為監測區,![]() 、
、![]() 為監測點(如圖).已知,
為監測點(如圖).已知,![]() 、
、![]() 、
、![]() 在同一條直線上,且
在同一條直線上,且![]() ,
,![]() 米,
米,![]() ,
,![]() .
.
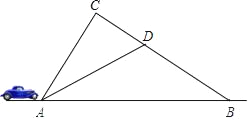
(1)求道路![]() 段的長;(精確到1米)
段的長;(精確到1米)
(2)如果![]() 段限速為60千米/時,一輛車通過
段限速為60千米/時,一輛車通過![]() 段的時間為90秒,請判斷該車是否超速,并說明理由.(參考數據:
段的時間為90秒,請判斷該車是否超速,并說明理由.(參考數據:![]()
![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,反比例函數y= ![]() 的圖象與一次函數y=x+b的圖象交
的圖象與一次函數y=x+b的圖象交
于點A(1,4)、點B(-4,n).

(1)求一次函數和反比例函數的解析式;
(2)求△OAB的面積;
(3)直接寫出一次函數值大于反比例函數值的自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,要在寬為22米的大道兩邊安裝路燈,路燈的燈臂CD長2米,且與燈柱BC成120°角,路燈采用圓錐形燈罩,燈罩的軸線DO與燈臂CD垂直,當燈罩的軸線DO通過公路路面的中心線時照明效果最佳,求路燈的燈柱BC高度.
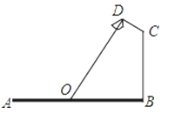
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從甲、乙兩位運動員中選出一名參加在規定時間內的投籃比賽.預先對這兩名運動員進行了6次測試,成績如下(單位:個):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均數 | 眾數 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根據測試成績,請你運用所學的統計知識作出分析,派哪一位運動員參賽更好?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店老板去圖書批發市場購買某種圖書,第一次用1200元購書若干本,并按該書定價7元出售,很快售完.由于該書暢銷,第二次購書時,每本書的批發價已比第一次提高了20%,他用1500元所購該書的數量比第一次多10本,當按定價售出200本時,出現滯銷,便以定價的4折售完剩余的書.
(1)第一次購書的進價是多少元?
(2)試問該老板這兩次售書總體上是賠錢了,還是賺錢了(不考慮其他因素)?若賠錢,賠多少;若賺錢,賺多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中有兩點![]() 、
、![]() ,我們定義
,我們定義![]() 、
、![]() 兩點間的“
兩點間的“![]() 值”直角距離為
值”直角距離為![]() ,且滿足
,且滿足![]() ,其中
,其中![]() .小靜和佳佳在解決問題:(求點
.小靜和佳佳在解決問題:(求點![]() 與點
與點![]() 的“1值”直角距離
的“1值”直角距離![]() )時,采用了兩種不同的方法:
)時,采用了兩種不同的方法:
(方法一):![]() ;
;
(方法二):如圖1,過點![]() 作
作![]() 軸于點
軸于點![]() ,過點
,過點![]() 作直線
作直線![]() 與
與![]() 軸交于點
軸交于點![]() ,則
,則![]()
請你參照以上兩種方法,解決下列問題:
(1)已知點![]() ,點
,點![]() ,則
,則![]() 、
、![]() 兩點間的“2值”直角距離
兩點間的“2值”直角距離![]() .
.
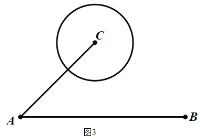
(2)函數![]() 的圖像如圖2所示,點
的圖像如圖2所示,點![]() 為其圖像上一動點,滿足
為其圖像上一動點,滿足![]() 兩點間的“
兩點間的“![]() 值”直角距離
值”直角距離![]() ,且符合條件的點
,且符合條件的點![]() 有且僅有一個,求出符合條件的“
有且僅有一個,求出符合條件的“![]() 值”和點
值”和點![]() 坐標.
坐標.
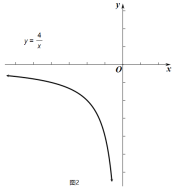
(3)城市的許多街道是相互垂直或平行的,因此,往往不能沿直線行走到達目的地,只能按直角拐彎的方式行走,因此,兩地之間修建垂直和平行的街道常常轉化為兩點間的“![]() 值”直角距離,
值”直角距離,![]() 地位于
地位于![]() 地的正東方向上,
地的正東方向上,![]() 地在
地在![]() 點東北方向上且相距
點東北方向上且相距![]() ,以
,以![]() 為圓心修建了一個半徑為
為圓心修建了一個半徑為![]() 的圓形濕地公園,現在要在公園和
的圓形濕地公園,現在要在公園和![]() 地之間修建觀光步道.步道只能東西或者南北走向,并且東西方向每千米成本是20萬元,南北方向每千米的成本是10萬元,問:修建這一規光步道至少要多少萬元?
地之間修建觀光步道.步道只能東西或者南北走向,并且東西方向每千米成本是20萬元,南北方向每千米的成本是10萬元,問:修建這一規光步道至少要多少萬元?

查看答案和解析>>
科目:初中數學 來源: 題型:
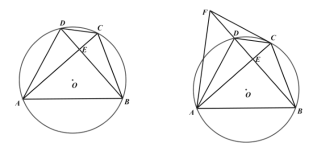
【題目】四邊形![]() 是
是![]() 的內接四邊形,
的內接四邊形,![]() ,
,![]() ,垂足為
,垂足為![]() .
.
(1)如圖1,求證:![]() ;
;
(2)如圖2,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,連接
,連接![]() 、
、![]() ,求證:
,求證:![]() ;
;
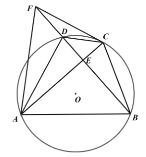
(3)如圖3,在(2)的條件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com