
在矩形ABCD中,AB = 10,BC = 12,E為DC的中點,
連接BE,作AF⊥BE,垂足為F.
(1)求證:△BEC∽△ABF;
(2)求AF的長.
 |
 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數學 來源: 題型:
如圖,四邊形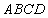 、
、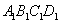 是兩個邊長分別為5和1且中心重合的正方形.其中,正方形
是兩個邊長分別為5和1且中心重合的正方形.其中,正方形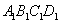 可以繞中心
可以繞中心 旋轉,正方形
旋轉,正方形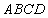 靜止不動.
靜止不動.
(1)如圖1,當 四點共線時,四邊形
四點共線時,四邊形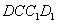 的面積為__;
的面積為__;
(2)如圖2,當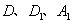 三點共線時,請直接寫
三點共線時,請直接寫 出
出 = _________;
= _________;
(3)在正方形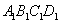 繞中心
繞中心 旋轉的過程中,直線
旋轉的過程中,直線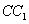 與直線
與直線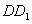 的位置關
的位置關 系是______________,請借助圖3證明你的猜想.
系是______________,請借助圖3證明你的猜想.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
.以平面上一點O為直角頂點,分別畫出兩個直角三角形,記作△AOB和△COD,
其中∠ABO=∠DCO=30°.
(1)點E、F、M分別是AC、CD、DB的中點,連接EF 和FM.
①如圖1,當點D、C分別在AO、BO的延長線上時,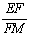 =_______;
=_______;
②如圖2,將圖1中的△AOB繞點O沿順時針方向旋轉 角(
角(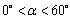 ),
),
其他條件不變,判斷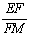 的值是否發生變化,并對你的結論進行證明;
的值是否發生變化,并對你的結論進行證明;
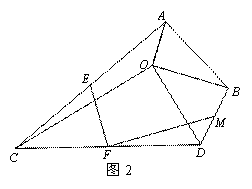 (2)如圖3,若BO=
(2)如圖3,若BO=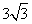 ,點N在線段OD上,且NO=3.點P是線段AB上的一個動點,在將△AOB繞點O旋轉的過程中,線段PN長度的最小值為_______,最大值為_______.
,點N在線段OD上,且NO=3.點P是線段AB上的一個動點,在將△AOB繞點O旋轉的過程中,線段PN長度的最小值為_______,最大值為_______.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
將拋物線y=(x﹣1)2+3向左平移1個單位,再向下平移3個單位后所得拋物線的解析式為( )
|
| A. y=(x﹣2)2 | B. | y=(x﹣2)2+6 | C. | y=x2+6 | D. | y=x2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
已知二次函數y=ax2+bx+c(a>0)的圖象與x軸交于A(x1,0)、B(x2,0)(x1<x2)兩點,與y軸交于點C,x1,x2是方程x2 +4x﹣5=0的兩根.
+4x﹣5=0的兩根.
(1)若拋物線的頂點為D,求S△ABC:S△ACD的值;
(2)若∠ADC=90°,求二次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
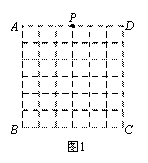
如圖1,正方形ABC D是一個6 × 6網格的示意圖,其中每個小正方形的邊長為1,位于AD中點處的點P按圖2的程序移動.
D是一個6 × 6網格的示意圖,其中每個小正方形的邊長為1,位于AD中點處的點P按圖2的程序移動.
(1)請在圖中畫出點P經過的路徑;
(2)求點P經過的路徑總長.
 | |||
 | |||
| |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com