
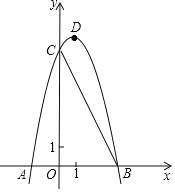
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,
點,![]() .
.
(1)求拋物線的表達(dá)式及其頂點![]() 的坐標(biāo);
的坐標(biāo);
(2)過點![]() 作
作![]() 軸的垂線,交直線
軸的垂線,交直線![]() 于點
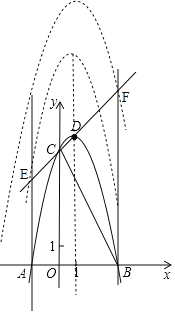
于點![]() ,將拋物線沿其對稱軸向上平移
,將拋物線沿其對稱軸向上平移![]() 個單位,使拋物線與線段
個單位,使拋物線與線段![]() (含線段端點)只有1個公共點.求
(含線段端點)只有1個公共點.求![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ;頂點坐標(biāo)為
;頂點坐標(biāo)為![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 、
、![]() 得點
得點![]() 坐標(biāo),將點
坐標(biāo),將點![]() 、
、![]() 坐標(biāo)代入求解可得;
坐標(biāo)代入求解可得;
(2)先求出直線![]() 解析式和點
解析式和點![]() 、
、![]() 坐標(biāo),設(shè)平移后解析式為
坐標(biāo),設(shè)平移后解析式為![]() ,結(jié)合圖象根據(jù)拋物線與線段
,結(jié)合圖象根據(jù)拋物線與線段![]() (含線段端點)只有1個公共點,求得臨界時
(含線段端點)只有1個公共點,求得臨界時![]() 的值,從而得出答案.
的值,從而得出答案.
(1)由拋物線的表達(dá)式知,點![]() ,即
,即![]() ;
;
![]() 中,
中,![]() ,
,
則點![]() .
.
將![]() 、
、![]() 的坐標(biāo)代入拋物線的表達(dá)式中,
的坐標(biāo)代入拋物線的表達(dá)式中,
得:![]() ,
,
解得:![]() ,
,
∴拋物線的表達(dá)式為![]() ,
,
∵![]() ,
,
∴拋物線的頂點坐標(biāo)為![]() .
.
(2)設(shè)直線![]() 的表達(dá)式為
的表達(dá)式為![]() ,
,
∵點![]() ,
,
∴直線![]() 表達(dá)式為
表達(dá)式為![]() .
.
∵過點![]() 、
、![]() 作
作![]() 軸的垂線,交直線
軸的垂線,交直線![]() 于點
于點![]() 、
、![]() ,
,
可得:![]() .
.
設(shè)拋物線向上平移![]() 個單位長度
個單位長度![]() ,
,
則拋物線的表達(dá)式為:![]() ;
;
當(dāng)拋物線過![]() 時,
時,![]() ,
,
當(dāng)拋物線過![]() 時,
時,![]() ,
,
∵拋物線與線段![]() (含線段端點)只有1個公共點,
(含線段端點)只有1個公共點,
∴![]() 的取值范圍是
的取值范圍是![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
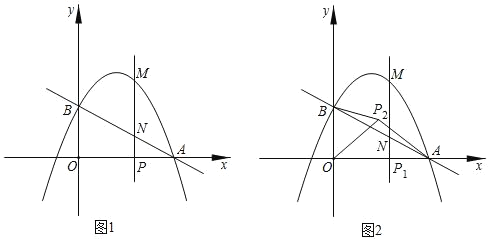
【題目】如圖1,拋物線y=ax2+(a+2)x+2(a≠0),與x軸交于點A(4,0),與y軸交于點B,在x軸上有一動點P(m,0)(0<m<4),過點P作x軸的垂線交直線AB于點N,交拋物線于點M.
(1)求拋物線的解析式;
(2)若PN:PM=1:4,求m的值;
(3)如圖2,在(2)的條件下,設(shè)動點P對應(yīng)的位置是P1,將線段OP1繞點O逆時針旋轉(zhuǎn)得到OP2,旋轉(zhuǎn)角為α(0°<α<90°),連接AP2、BP2,求AP2+![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】春節(jié)期間某商場搞促銷活動,方案是:在一個不透明的箱子里放4個完全相同的小球,球上分別標(biāo)“0元”、“20元”、“30元”、“50元”,顧客每消費滿300元,就可從箱子里同時摸出兩個球,根據(jù)這兩個小球所標(biāo)金額之和可獲相應(yīng)價格的禮品;
(1)若某顧客在甲商商場消費320元,至少可得價值______元的禮品,至多可得價值______元的禮品;
(2)請用畫樹狀圖或列表的方法,求該顧客去商場消費,獲得禮品的總價值不低于50元的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
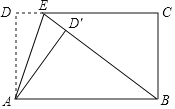
【題目】如圖,已知E為長方形紙片ABCD的邊CD上一點,將紙片沿AE對折,點D的對應(yīng)點D′恰好在線段BE上.若AD=3,DE=1,則AB=_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
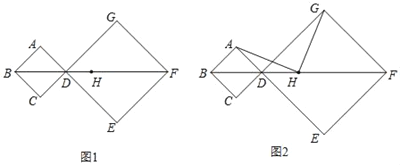
【題目】在正方形ABCD和正方形DEFG中,頂點B、D、F在同一直線上,H是BF的中點.
(1)如圖1,若AB=1,DG=2,求BH的長;
(2)如圖2,連接AH,GH.
小宇觀察圖2,提出猜想:AH=GH,AH⊥GH.小宇把這個猜想與同學(xué)們進(jìn)行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:延長AH交EF于點M,連接AG,GM,要證明結(jié)論成立只需證△GAM是等腰直角三角形;
想法2:連接AC,GE分別交BF于點M,N,要證明結(jié)論成立只需證△AMH≌△HNG.…
請你參考上面的想法,幫助小宇證明AH=GH,AH⊥GH.(一種方法即可)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列材料:
延慶是全市唯一一個全境域都是水源保護(hù)地的區(qū)域,森林覆蓋率達(dá)到57.46%,“干凈指數(shù)”連續(xù)五年全市第一,人均公共綠地面積41.88平方米,空氣質(zhì)量長期保持全市前列.根據(jù)區(qū)環(huán)保局的空氣質(zhì)量的通報,2012年空氣質(zhì)量為優(yōu),成為北京市最宜居的地方.
由于經(jīng)濟(jì)發(fā)展,私家車劇增等原因,2013年空氣質(zhì)量下降為良,尤其是PM2.5平均濃度有所增長,2013年PM2.5平均濃度約為78微克/立方米,比2012年PM2.5平均濃度增長了12.2%.延慶區(qū)作為2019年世園會和2022年冬奧會比賽的舉辦地,將全面治理“煤、氣、塵”,逐漸降低PM2.5濃度,力爭到2020年降至46微克/立方米,實現(xiàn)“延慶藍(lán)”.
據(jù)悉,延慶將大力推廣地源熱泵、風(fēng)能、太陽能等新能源和可再生能源.同時強化大貨車監(jiān)管,提升新能源車輛利用率.2020年新能源和可再生能源在延慶的使用比例將達(dá)到40%,煤炭能源消費總量占比3%以下,基本建成“無煤區(qū)”.
經(jīng)過全面治理,2014年PM2.5平均濃度約為70微克/立方米,比2013年平均濃度降低了10.26%;2015年PM2.5平均濃度比2014年平均濃度降低了10%,為全市最低;2016年PM2.5平均濃度約為56微克/立方米.
根據(jù)以上材料解答下列問題:
(1)2015年PM2.5平均濃度約為 微克/立方米;
(2)選擇統(tǒng)計表或統(tǒng)計圖,將2013﹣2016年PM2.5平均濃度整理出來;
(3)根據(jù)上述材料和繪制的統(tǒng)計表或統(tǒng)計圖中提供的信息,預(yù)估2017年的PM2.5平均濃度約為 微克/立方米;你的預(yù)估理由是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1.![]() 的半徑為
的半徑為![]() ,若點
,若點![]() 在射線
在射線![]() 上,且
上,且![]() ,則稱點
,則稱點![]() 是點
是點![]() 關(guān)于
關(guān)于![]() 的“反演點”,如圖2,
的“反演點”,如圖2,![]() 的半徑為2,點
的半徑為2,點![]() 在
在![]() 上.
上.![]() ,
,![]() ,若點
,若點![]() 是點
是點![]() 關(guān)于
關(guān)于![]() 的反演點,點
的反演點,點![]() 是點
是點![]() 關(guān)于
關(guān)于![]() 的反演點,則
的反演點,則![]() 的長為( )
的長為( )
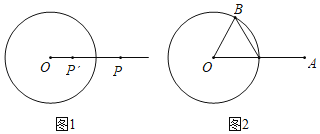
A.![]() B.
B.![]() C.2D.4
C.2D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我們規(guī)定:平面內(nèi)點A到圖形G上各個點的距離的最小值稱為該點到這個圖形的最小距離d,點A到圖形G上各個點的距離的最大值稱為該點到這個圖形的最大距離D,定義點A到圖形G的距離跨度為R=D-d.
(1)①如圖1,在平面直角坐標(biāo)系xOy中,圖形G1為以O為圓心,2為半徑的圓,直接寫出以下各點到圖形G1的距離跨度:
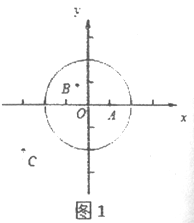
A(1,0)的距離跨度______________;
B(-![]() ,
, ![]() )的距離跨度____________;
)的距離跨度____________;
C(-3,-2)的距離跨度____________;
②根據(jù)①中的結(jié)果,猜想到圖形G1的距離跨度為2的所有的點組成的圖形的形狀是______________.
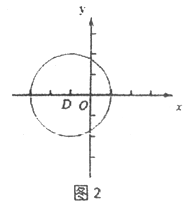
(2)如圖2,在平面直角坐標(biāo)系xOy中,圖形G2為以D(-1,0)為圓心,2為半徑的圓,直線y=k(x-1)上存在到G2的距離跨度為2的點,求k的取值范圍.
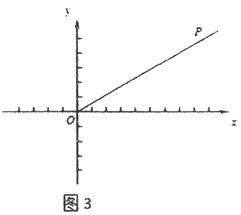
(3)如圖3,在平面直角坐標(biāo)系xOy中,射線OP:y=![]() x(x≥0),⊙E是以3為半徑的圓,且圓心E在x軸上運動,若射線OP上存在點到⊙E的距離跨度為2,求出圓心E的橫坐標(biāo)xE的取值范圍.
x(x≥0),⊙E是以3為半徑的圓,且圓心E在x軸上運動,若射線OP上存在點到⊙E的距離跨度為2,求出圓心E的橫坐標(biāo)xE的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
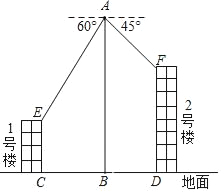
【題目】如圖,某興趣小組用無人機進(jìn)行航拍測高,無人機從1號樓和2號樓的地面正中間B點垂直起飛到高度為50米的A處,測得1號樓頂部E的俯角為60°,測得2號樓頂部F的俯角為45°.已知1號樓的高度為20米,則2號樓的高度為_____米(結(jié)果保留根號).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com