
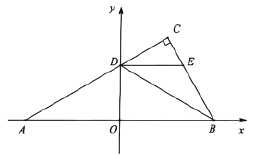
【題目】如圖平面直角坐標(biāo)系中,點![]() ,
,![]() 在
在![]() 軸上,
軸上,![]() ,點
,點![]() 在
在![]() 軸上方,
軸上方,![]() ,
,![]() ,線段
,線段![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() ,連接
,連接![]() ,
,![]() 平分
平分![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于
于![]() .
.
(1)點![]() 的坐標(biāo)為 .
的坐標(biāo)為 .
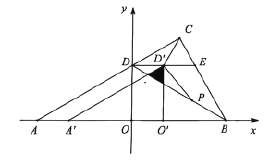
(2)將![]() 沿線段
沿線段![]() 向右平移得
向右平移得![]() ,當(dāng)點
,當(dāng)點![]() 與
與![]() 重合時停止運(yùn)動,記
重合時停止運(yùn)動,記![]() 與
與![]() 的重疊部分面積為
的重疊部分面積為![]() ,點
,點![]() 為線段
為線段![]() 上一動點,當(dāng)
上一動點,當(dāng)![]() 時,求
時,求![]() 的最小值;
的最小值;
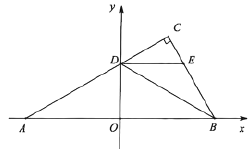
(3)當(dāng)![]() 移動到點
移動到點![]() 與
與![]() 重合時,將
重合時,將![]() 繞點
繞點![]() 旋轉(zhuǎn)一周,旋轉(zhuǎn)過程中,直線
旋轉(zhuǎn)一周,旋轉(zhuǎn)過程中,直線![]() 分別與直線
分別與直線![]() 、直線
、直線![]() 交于點
交于點![]() 、點
、點![]() ,作點
,作點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點
的對稱點![]() ,連接
,連接![]() 、
、![]() 、
、![]() .當(dāng)
.當(dāng)![]() 為直角三角形時,直接寫出線段
為直角三角形時,直接寫出線段![]() 的長.
的長.
【答案】(1)C(3,3![]() );(2)最小值為2+2
);(2)最小值為2+2![]() ;(3)D0H的值為2
;(3)D0H的值為2![]() -2或2
-2或2![]() +2或4
+2或4![]() -4或4
-4或4![]() +4.
+4.
【解析】
(1)想辦法求出A,D,B的坐標(biāo),求出直線AC,BC的解析式,構(gòu)建方程組即可解決問題.
(2)如圖2中,設(shè)BD交O′D′于G,交A′D′于F.作PH⊥OB于H.利用三角形的面積公式求出點D坐標(biāo),再證明PH=![]() PB,把問題轉(zhuǎn)化為垂線段最短即可解決問題.
PB,把問題轉(zhuǎn)化為垂線段最短即可解決問題.
(3)在旋轉(zhuǎn)過程中,符號條件的△GD0H有8種情形,分別畫出圖形一一求解即可.
(1)如圖1中,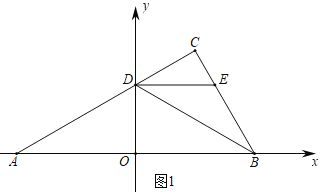
在Rt△AOD中,∵∠AOD=90°,∠OAD=30°,OD=2![]() ,
,
∴OA=![]() OD=6,∠ADO=60°,
OD=6,∠ADO=60°,
∴∠ODC=120°,
∵BD平分∠ODC,
∴∠ODB=![]() ∠ODC=60°,
∠ODC=60°,
∴∠DBO=∠DAO=30°,
∴DA=DB=4![]() ,OA=OB=6,
,OA=OB=6,
∴A(-6,0),D(0,2![]() ),B(6,0),
),B(6,0),
∴直線AC的解析式為y=![]() x+2
x+2![]() ,
,
∵AC⊥BC,
∴直線BC的解析式為y=-![]() x+6
x+6![]() ,
,
由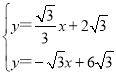 ,解得
,解得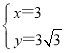 ,
,
∴C(3,3![]() ).
).
(2)如圖2中,設(shè)BD交O′D′于G,交A′D′于F.作PH⊥OB于H.
∵∠FD′G=∠D′GF=60°,
∴△D′FG是等邊三角形,
∵S△D′FG=![]() ,
,
∴D′G=![]() ,
,
∴DD′=![]() GD′=2,
GD′=2,
∴D′(2,2![]() ),
),
∵C(3,3![]() ),
),
∴CD′=![]() =2,
=2,
在Rt△PHB中,∵∠PHB=90°,∠PBH=30°,
∴PH=![]() PB,
PB,
∴CD'+D'P+![]() PB=2+D′P+PH≤2+D′O′=2+2
PB=2+D′P+PH≤2+D′O′=2+2![]() ,
,
∴CD'+D'P+![]() PB的最小值為2+2
PB的最小值為2+2![]() .
.
(3)如圖3-1中,當(dāng)D0H⊥GH時,連接ED0.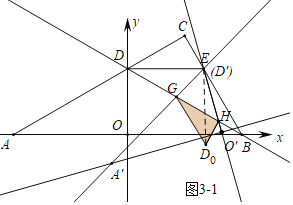
∵ED=ED0,EG=EG.DG=D0G,
∴△EDG≌△ED0G(SSS),
∴∠EDG=∠ED0G=30°,∠DEG=∠D0EG,
∵∠DEB=120°,∠A′EO′=60°,
∴∠DEG+∠BEO′=60°,
∵∠D0EG+∠D0EO′=60°,
∴∠D0EO′=∠BEO′,
∵ED0=EB,E=EH,
∴△EO′D0≌△EO′B(SAS),
∴∠ED0H=∠EBH=30°,HD0=HB,
∴∠CD0H=60°,
∵∠D0HG=90°,
∴∠D0GH=30°,設(shè)HD0=BH=x,則DG=GD0=2x,GH=![]() x,
x,
∵DB=4![]() ,
,
∴2x+![]() x+x=4
x+x=4![]() ,
,
∴x=2![]() -2.
-2.
如圖3-2中,當(dāng)∠D0GH=90°時,同法可證∠D0HG=30°,易證四邊形DED0H是等腰梯形,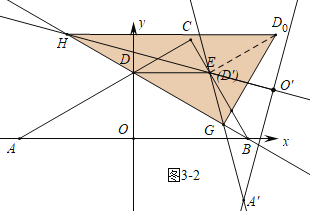
∵DE=ED0=DH=4,可得D0H=4+2×4×cos30°=4+4![]() .
.
如圖3-3中,當(dāng)D0H⊥GH時,同法可證:∠D0GH=30°,
在△EHD0中,由∠D0HE=45°,∠HD0E=30°,ED0=4,可得D0H=4×![]() ,
,
如圖3-4中,當(dāng)DG⊥GH時,同法可得∠D0HG=30°,
設(shè)DG=GD0=x,則HD0=BH=2x,GH=![]() x,
x,
∴3x+![]() x=4
x=4![]() ,
,
∴x=2![]() -2,
-2,
∴D0H=2x=4![]() -4.
-4.
如圖3-5中,當(dāng)D0H⊥GH時,同法可得D0H=2![]() -2.
-2.
如圖3-6中,當(dāng)DGG⊥GH時,同法可得D0H=4![]() +4.
+4.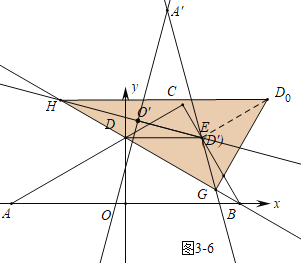
如圖3-7中,如圖當(dāng)D0H⊥HG時,同法可得D0H=2![]() +2.
+2.
如圖3-8中,當(dāng)D0G⊥GH時,同法可得HD0=4![]() -4.
-4.
綜上所述,滿足條件的D0H的值為2![]() -2或2
-2或2![]() +2或4
+2或4![]() -4或4
-4或4![]() +4.
+4.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導(dǎo)學(xué)與測試系列答案
導(dǎo)學(xué)與測試系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知△ABC∽△DEF,且相似比為k,則k=________,直線y=kx+k的圖象必經(jīng)過________象限.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
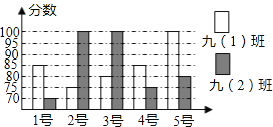
【題目】我區(qū)某中學(xué)開展“社會主義核心價值觀”演講比賽活動,九(1)、九(2)班根據(jù)初賽成績各選出5名選手參加復(fù)賽,兩個班各選出的5名選手的復(fù)賽成績(滿分為100分)如圖所示.根據(jù)圖中數(shù)據(jù)解決下列問題:
(1)九(1)班復(fù)賽成績的中位數(shù)是 分,九(2)班復(fù)賽成績的眾數(shù)是 分;
(2)小明同學(xué)已經(jīng)算出了九(1)班復(fù)賽的平均成績![]() =85分;方差S2=
=85分;方差S2=![]() [(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),請你求出九(2)班復(fù)賽的平均成績x2和方差S22;
[(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),請你求出九(2)班復(fù)賽的平均成績x2和方差S22;
(3)根據(jù)(2)中計算結(jié)果,分析哪個班級的復(fù)賽成績較好?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一個不透明的袋子中裝有三個完全相同的小球,分別標(biāo)有數(shù)字3、4、5.從袋子中隨機(jī)取出一個小球,用小球上的數(shù)字作為十位的數(shù)字,然后放回;再取出一個小球,用小球上的數(shù)字作為個位上的數(shù)字,這樣組成一個兩位數(shù),試問:按這種方法能組成哪些位數(shù)?十位上的數(shù)字與個位上的數(shù)字之和為9的兩位數(shù)的概率是多少?用列表法或畫樹狀圖法加以說明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
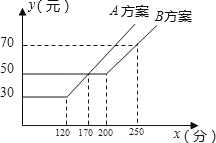
【題目】如圖,某電信公司提供了A,B兩種方案的移動通訊費(fèi)用y(元)與通話時間x(元)之間的關(guān)系,則下列結(jié)論中正確的有( )
(1)若通話時間少于120分,則A方案比B方案便宜20元;
(2)若通話時間超過200分,則B方案比A方案便宜12元;
(3)若通訊費(fèi)用為60元,則B方案比A方案的通話時間多;
(4)若兩種方案通訊費(fèi)用相差10元,則通話時間是145分或185分.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
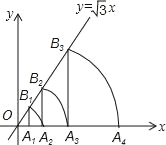
【題目】如圖,已知直線y=![]() x,點A1的坐標(biāo)為(1,0),過點A1作x軸的垂線交直線于點B1,以原點O為圓心,OB1的長為半徑畫弧交x軸于點A2;再過點A2作x軸的垂線交直線于點B2,以原點O為圓心,OB2的長為半徑畫弧交x軸于點A3,…,按此做法進(jìn)行下去,求點B6的坐標(biāo).
x,點A1的坐標(biāo)為(1,0),過點A1作x軸的垂線交直線于點B1,以原點O為圓心,OB1的長為半徑畫弧交x軸于點A2;再過點A2作x軸的垂線交直線于點B2,以原點O為圓心,OB2的長為半徑畫弧交x軸于點A3,…,按此做法進(jìn)行下去,求點B6的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,一次函數(shù)![]() 的圖象與
的圖象與![]() 軸負(fù)半軸交于點
軸負(fù)半軸交于點![]() ,與
,與![]() 軸正半軸交于點
軸正半軸交于點![]() ,點
,點![]() 為直線
為直線![]() 上一點,
上一點,![]() ,點
,點![]() 為
為![]() 軸正半軸上一點,連接
軸正半軸上一點,連接![]() ,
,![]() 的面積為48.
的面積為48.
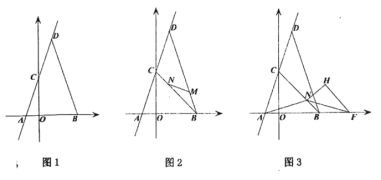
(1)如圖1,求點![]() 的坐標(biāo);
的坐標(biāo);
(2)如圖2,點![]() 分別在線段
分別在線段![]() 上,連接
上,連接![]() ,點
,點![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() ,點
,點![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() ,求
,求![]() 與
與![]() 的函數(shù)關(guān)系式(不要求寫出自變量
的函數(shù)關(guān)系式(不要求寫出自變量![]() 的取值范圍);
的取值范圍);
(3)在(2)的條件下,如圖3,連接![]() ,點
,點![]() 為
為![]() 軸正半軸上點
軸正半軸上點![]() 右側(cè)一點,點
右側(cè)一點,點![]() 為第一象限內(nèi)一點,
為第一象限內(nèi)一點,![]() ,
,![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,點
,點![]() 為
為![]() 上一點,直線
上一點,直線![]() 經(jīng)過點
經(jīng)過點![]() 和點
和點![]() ,過點
,過點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() ,連接
,連接![]() ,請你判斷四邊形
,請你判斷四邊形![]() 的形狀,并說明理由.
的形狀,并說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com