
【題目】我們知道:點A、B在數(shù)軸上分別表示有理數(shù)a、b,如圖A、B兩點之間的距離表示為AB,記作AB=|a﹣b|.回答下列問題:
(1)數(shù)軸上表示2和5兩點之間的距離是 ,數(shù)軸上表示1和﹣3的兩點之間的距離是 ;
(2)已知|a﹣3|=7,則有理數(shù)a= ;
(3)若數(shù)軸上表示數(shù)b的點位于﹣4與3的兩點之間,則|b﹣3|+|b+4|= .
![]()
【答案】(1)3,4;(2)10或-4;(3)7
【解析】
(1)根據(jù)AB=|a﹣b|解答;
(2)去絕對值計算;
(3)根據(jù)絕對值的性質(zhì)去掉絕對值符號,然后計算即可得解.
解:(1)數(shù)軸上表示2和5兩點之間的距離是:|5﹣2|=3,數(shù)軸上表示1和﹣3的兩點之間的距離是:|﹣3﹣1|=4.
故答案是:3;4;
(2)依題意得:a﹣3=7,或a﹣3=﹣7,
解得a=10或a=﹣4,
故答案是:10或﹣4;
(3)若數(shù)軸上表示數(shù)b的點位于﹣4與3的兩點之間,∴-4<b<3;則|b﹣3|+|b+4|=3﹣b+b+4=7.
故答案是:7.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+bx+c與x軸交于點A(﹣1,0)和點B(3,0),與y軸交于點C,連接BC交拋物線的對稱軸于點E,D是拋物線的頂點.
(1)求此拋物線的解析式;
(2)直接寫出點C和點D的坐標;
(3)若點P在第一象限內(nèi)的拋物線上,且S△ABP=4S△COE , 求P點坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】自2017年3月起,成都市中心城區(qū)居民用水實行以戶為單位的三級階梯收費辦法:
第I級:居民每戶每月用水18噸以內(nèi)含18噸每噸收水費a元;
第Ⅱ級:居民每戶每月用水超過18噸但不超過25噸,未超過18噸的部分按照第Ⅰ級標準收費,超過部分每噸收水費b元;
第Ⅲ級:居民每戶每月用水超過25噸,未超過25噸的部分按照第I、Ⅱ級標準收費,超過部分每噸收水費c元.
設一戶居民月用水x噸,應繳水費為y元,y與x之間的函數(shù)關系如圖所示
(1)根據(jù)圖象直接作答:a= ,b= ;
(2)求當x≥25時y與x之間的函數(shù)關系;
(3)把上述水費階梯收費辦法稱為方案①,假設還存在方案②:居民每戶月用水一律按照每噸4元的標準繳費,請你根據(jù)居民每戶月“用水量的大小設計出對居民繳費最實惠的方案.(寫出過程)

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
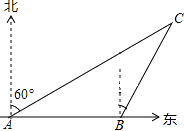
【題目】如圖,一漁船自西向東追趕魚群,在A處測得某無名小島C在北偏東60°方向上,前進2海里到達B點,此時測得無名小島C在東北方向上.已知無名小島周圍2.5海里內(nèi)有暗礁,問漁船繼續(xù)追趕魚群有無觸礁危險?(參考數(shù)據(jù): ![]() )
)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】操作與思考:一張邊長為a的正方形桌面,因為實際需要,需將正方形邊長增加b,從而得到一個更大的正方形,木工師傅設計了如圖所示的方案:
(1)方案中大正方形的邊長都是 ,所以面積為 ;
(2)小明還發(fā)現(xiàn):方案中大正方形的面積還可以用四塊小四邊形的面積和來表示 ;
(3)你有什么發(fā)現(xiàn),請用數(shù)學式子表達 ;
(4)利用(3)的結(jié)論計算20.182+2×20.18×19.82+19.822的值.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數(shù) ![]() (m為常數(shù))的圖象與x軸交于點A(﹣3,0),與y軸交于點C.以直線x=1為對稱軸的拋物線y=ax2+bx+c(a,b,c為常數(shù),且a≠0)經(jīng)過A,C兩點,并與x軸的正半軸交于點B.
(m為常數(shù))的圖象與x軸交于點A(﹣3,0),與y軸交于點C.以直線x=1為對稱軸的拋物線y=ax2+bx+c(a,b,c為常數(shù),且a≠0)經(jīng)過A,C兩點,并與x軸的正半軸交于點B.
(1)求m的值及拋物線的函數(shù)表達式;
(2)設E是y軸右側(cè)拋物線上一點,過點E作直線AC的平行線交x軸于點F.是否存在這樣的點E,使得以A,C,E,F(xiàn)為頂點的四邊形是平行四邊形?若存在,求出點E的坐標及相應的平行四邊形的面積;若不存在,請說明理由;
(3)若P是拋物線對稱軸上使△ACP的周長取得最小值的點,過點P任意作一條與y軸不平行的直線交拋物線于M1(x1 , y1),M2(x2 , y2)兩點,試探究 ![]() 是否為定值,并寫出探究過程.
是否為定值,并寫出探究過程.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某服裝店購進一批甲、乙兩種款型時尚T恤衫,甲種款型共用了7800元,乙種款型共用了6400元,甲種款型的件數(shù)是乙種款型件數(shù)的1.5倍,甲種款型每件的進價比乙種款型每件的進價少30元.
(1)甲、乙兩種款型的T恤衫各購進多少件?
(2)商店進價提高60%標價銷售,銷售一段時間后,甲款型全部售完,乙款型剩余一半,商店決定對乙款型按標價的五折降價銷售,很快全部售完,求售完 這批T恤衫商店共獲利多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知拋物線y= ![]() x2+mx+n(n≠0)與直線y=x交于A、B兩點,與y軸交于點C,OA=OB,BC∥x軸.
x2+mx+n(n≠0)與直線y=x交于A、B兩點,與y軸交于點C,OA=OB,BC∥x軸.
(1)求拋物線的解析式;
(2)設D、E是線段AB上異于A、B的兩個動點(點E在點D的上方),DE= ![]() ,過D、E兩點分別作y軸的平行線,交拋物線于F、G,若設D點的橫坐標為x,四邊形DEGF的面積為y,求x與y之間的關系式,寫出自變量x的取值范圍,并回答x為何值時,y有最大值.
,過D、E兩點分別作y軸的平行線,交拋物線于F、G,若設D點的橫坐標為x,四邊形DEGF的面積為y,求x與y之間的關系式,寫出自變量x的取值范圍,并回答x為何值時,y有最大值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com