
【題目】如圖,ABCD的對角線AC,BD交于點O,AE平分∠BAD交BC于點E,且∠ADC=60°,AB=![]() BC,連結OE.下列結論:
BC,連結OE.下列結論:
①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=![]() BC,成立的結論有______.(填序號)
BC,成立的結論有______.(填序號)
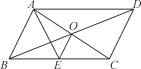
【答案】①②④
【解析】
由四邊形ABCD是平行四邊形,得到∠ABC=∠ADC=60°,∠BAD=120°,根據AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等邊三角形,由于AB=![]() BC,得到AE=
BC,得到AE=![]() BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正確;由于AC⊥AB,得到SABCD=ABAC,故②正確,根據AB=
BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正確;由于AC⊥AB,得到SABCD=ABAC,故②正確,根據AB=![]() BC,OB=
BC,OB=![]() BD,且BD>BC,得到AB≠OB,故③錯誤;根據三角形的中位線定理得到OE=
BD,且BD>BC,得到AB≠OB,故③錯誤;根據三角形的中位線定理得到OE=![]() AB,于是得到OE=
AB,于是得到OE=![]() BC,故④正確.
BC,故④正確.
∵四邊形ABCD是平行四邊形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等邊三角形,
∴AE=AB=BE,
∵AB=![]() BC,
BC,
∴AE=![]() BC,
BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正確;
∵AC⊥AB,
∴SABCD=ABAC,故②正確,
∵AB=![]() BC,OB=
BC,OB=![]() BD,
BD,
∵BD>BC,
∴AB≠OB,故③錯誤;
∵CE=BE,CO=OA,
∴OE=![]() AB,
AB,
∴OE=![]() BC,故④正確.
BC,故④正確.
故答案為:①②④.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒1cm,設出發的時間為t秒.

(1)出發2秒后,求△ABP的周長.
(2)問t滿足什么條件時,△BCP為直角三角形?
(3)另有一點Q,從點C開始,按C→B→A→C的路徑運動,且速度為每秒2cm,若P、Q兩點同時出發,當P、Q中有一點到達終點時,另一點也停止運動.當t為何值時,直線PQ把△ABC的周長分成相等的兩部分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一副直角三角板如圖放置,使含30°角的三角板的直角邊和含45°角的三角板的一條直角邊在同一條直線上,則∠1的度數為( ) 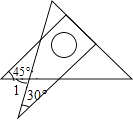
A.75°
B.65°
C.45°
D.30°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知長方形ABCO中,邊AB=12,BC=8.以點0為原點,OA、OC所在的直線為y軸和x軸建立直角坐標系.
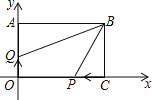
(1)點A的坐標為(0,8),寫出B.C兩點的坐標;
(2)若點P從C點出發,以3單位/秒的速度向CO方向移動(不超過點O),點Q從原點O出發,以2單位/秒的速度向OA方向移動(不超過點A),設P、Q兩點同時出發,在它們移動過程中,四邊形OPBQ的面積是否發生變化?若不變,求其值;若變化,求變化范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)化簡求值:(2+a)(2-a)+a(a-2b)+3a5b÷(-a2b)4,其中ab=-![]() .
.
(2)因式分解:a(n-1)2-2a(n-1)+a.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列多項式的乘法中,能用平方差公式計算的是( )
A. (-m +n)(m - n) B. (![]() a +b)(b -
a +b)(b -![]() a)
a)
C. (x + 5)(x + 5) D. (3a -4b)(3b +4a)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C在AB的延長線上,CD與⊙O相切于點D,CE⊥AD,交AD的延長線于點E. 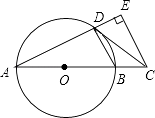
(1)求證:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國古代數學家們對于勾股定理的發現和證明,在世界數學史上具有獨特的貢獻和地位,體現了數學研究中的繼承和發展.現用4個全等的直角三角形拼成如圖所示“弦圖”.Rt△ABC中,∠ACB=90°,若![]() ,請你利用這個圖形解決下列問題:
,請你利用這個圖形解決下列問題:
(1)試說明![]() ;
;
(2)如果大正方形的面積是10,小正方形的面積是2,求![]() 的值.
的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com