
【題目】如圖,M、N是邊長為6的正方形ABCD的邊CD上的兩個動點,滿足AM=BN,連接AC交BN于點E,連接DE交AM于點F,連接CF.
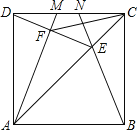
(1)求證:DE=BE;
(2)判斷DE與AM的位置關系,并證明;
(3)判斷線段CF是否存在最小值?若存在,求出來,若不存在,說明理由.
【答案】(1)見解析;(2)DE⊥AM,見解析;(3)存在最小值,最小值為![]() .
.
【解析】
(1)證明△DAE≌△BAE(SAS)即可解決問題.
(2)想辦法證明∠DAM=∠EDC即可.
(3)存在最小值.如圖,取AD的中點O,連接OF、OC,利用三角形三邊關系解決問題即可.
解:(1)證明:在正方形ABCD中,AD=AB,∠DAE=BAE,又AE為公共邊,
∴△DAE≌△BAE(SAS),
∴DE=BE.
(2)結論:互相垂直.
理由::在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD=90°,
∵AM=BN,
∴Rt△ADM≌Rt△BCN(HL),
∴∠DAM=∠CBN
由(1)知DE=BE,又CD=CB,CE為公共邊,
∴△DCE≌△BCE(SSS),
∴∠CDE=∠CBE
∵∠ADF+∠CDE=∠ADC=90°
∴∠DAF+∠ADF=90°
∴∠DFA=180°﹣90°=90°
即DE⊥AM.
(3)存在最小值.如圖,取AD的中點O,連接OF、OC,
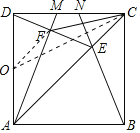
則OF=DO=![]() AD=3,
AD=3,
在Rt△OCD中,
OC=![]() ,
,
根據三角形的三邊關系,OF+CF>OC,
∴當O、F、C三點共線時,CF的長度最小,最小值為OC﹣OF=![]() .
.


科目:初中數學 來源: 題型:
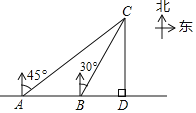
【題目】今年“五一”期間,小明一家到某農莊采摘,在村口A處,小明接到農莊發來的定位,發現農莊C在自己的北偏東45°方向,于是沿河邊筆直綠道l步行200米到達B處,此時定位顯示農莊C在自己的北偏東30°方向,電話聯系,得知農莊主已到農莊C正南方的橋頭D處等待,請問還要沿綠道直走多少米才能到達橋頭D處.(精確到1米,參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC繞點C順時針旋轉36°,點B的對應點為點E,點A的對應點為點D,此時點E恰好落在邊AC上時,連接AD,若AB=BC,AC=2,則AB的長度是( )
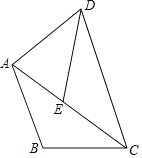
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖分別是五角星、六角星、七角星、八角星的圖形;
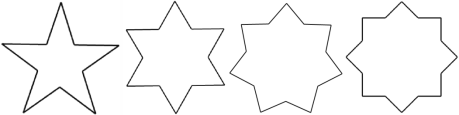
(1)請問其中是中心對稱圖形的是哪些?
(2)依次類推,36角星是不是中心對稱圖形?
(3)怎樣判斷一個n角星是否是中心對稱圖形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場服裝部為了解服裝的銷售情況,統計了每位營業員在某月的銷售額(單位:萬元),并根據統計的這組銷售額數據,繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:
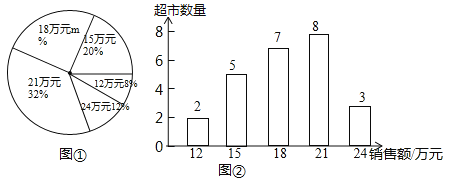
(Ⅰ)該商場服裝部營業員的人數為_____________,圖①中![]() 的值為____________;
的值為____________;
(Ⅱ)求統計的這組銷售額數據的平均數、眾數和中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
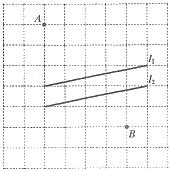
【題目】如圖,在每個小正方形的邊長為1的網格中,點![]() 均在格點上,
均在格點上,![]() 是一條小河平行的兩岸.
是一條小河平行的兩岸.
(Ⅰ)![]() 的距離等于_____;
的距離等于_____;
(Ⅱ)現要在小河上修一座垂直于兩岸的橋![]() (點
(點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,橋的寬度忽略),使
上,橋的寬度忽略),使![]() 最短,請在如圖所示的網格中,用無刻度的直尺,畫出
最短,請在如圖所示的網格中,用無刻度的直尺,畫出![]() ,并簡要說明點
,并簡要說明點![]() ,
,![]() 的位置是如何找到的(不要求證明)_________________________________.
的位置是如何找到的(不要求證明)_________________________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com