
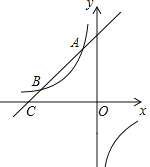
【題目】如圖,一次函數y=x+b的圖象與反比例函數y=![]() (k為常數且k≠0)的圖象交于A(﹣1,a)、B兩點,與x軸交于點C(﹣4,0).
(k為常數且k≠0)的圖象交于A(﹣1,a)、B兩點,與x軸交于點C(﹣4,0).
(1)求一次函數和反比例函數的表達式;
(2)若點D是第四象限內反比例函數圖象上的點,且點D到直線AC的距離為5![]() ,求點D的橫坐標.
,求點D的橫坐標.
【答案】(1)y=x+4;y=﹣![]() ;(2)點D的橫坐標x=±
;(2)點D的橫坐標x=±![]() +3.
+3.
【解析】
(1)將點C坐標代入y=x+b可得其解析式,將A的坐標代入一次函數和反比例函數解析式可得k的值,從而得出反比例函數解析式;
(2)過點D作DE∥AC交x軸于點E,過點E作EF⊥AC于點F,設直線DE的解析式為y=x+m,EF=5![]() ,由題意得出CO=GO=4知CE=
,由題意得出CO=GO=4知CE=![]() EF=10,EO=6,從而得E(6,0),將E(6,0)代入y=x+m中得m=﹣6,從而得出y=x﹣6,聯立
EF=10,EO=6,從而得E(6,0),將E(6,0)代入y=x+m中得m=﹣6,從而得出y=x﹣6,聯立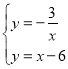 解之可得答案.
解之可得答案.
解:(1)將C(﹣4,0)代入y=x+b,得b=4,
∴一次函數的表達式為y=x+4,
將A(﹣1,a)代入y=x+4,y=![]() 中,得:a=﹣1+4,a=
中,得:a=﹣1+4,a=![]() ,
,
∴k=﹣3,
∴反比例函數的表達式為y=﹣![]() ;
;
(2)過點D作DE∥AC交x軸于點E,過點E作EF⊥AC于點F,
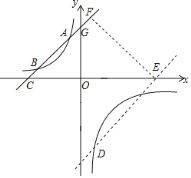
∴設直線DE的解析式為y=x+m,EF=5![]() ,
,
∵y=x+4,x=0時,y=4,
∴G(0,4),
又C(﹣4,0),
∴CO=GO=4,
又∠GOC=90°,
∴∠GCO=45°,
又∵EF⊥AC,
∴CE=![]() EF=10,
EF=10,
∴EO=EC-CO=6,
∴E(6,0),
將E(6,0)代入y=x+m中,得:m=﹣6,
∴y=x﹣6,
聯立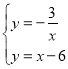 ,
,
解得x=![]() +3,
+3,
∴點D的橫坐標為![]() +3或-
+3或-![]() +3.
+3.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】某電器超市銷售每臺進價分別為2000元、1700元的A、B兩種型號的空調,如表是近兩周的銷售情況:
銷售時段 | 銷售數量 | 銷售收入 | |
A種型號 | B種型號 | ||
第一周 | 3臺 | 5臺 | 18000元 |
第二周 | 4臺 | 10臺 | 31000元 |
(進價、售價均保持不變,利潤=銷售總收入進貨成本)
(1)求A、B兩種型號的空調的銷售單價;
(2)若超市準備用不多于54000元的金額再采購這兩種型號的空調共30臺,求A種型號的空調最多能采購多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
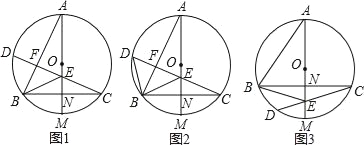
【題目】已知AM是⊙O直徑,弦BC⊥AM,垂足為點N,弦CD交AM于點E,連按AB和BE.
(1)如圖1,若CD⊥AB,垂足為點F,求證:∠BED=2∠BAM;
(2)如圖2,在(1)的條件下,連接BD,若∠ABE=∠BDC,求證:AE=2CN;
(3)如圖3,AB=CD,BE:CD=4:7,AE=11,求EM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點到直線的距離即為點到直線的垂線段的長.

(1)如圖1,取點M(1,0),則點M到直線l:y=![]() x﹣1的距離為多少?
x﹣1的距離為多少?
(2)如圖2,點P是反比例函數y=![]() 在第一象限上的一個點,過點P分別作PM⊥x軸,作PN⊥y軸,記P到直線MN的距離為d0,問是否存在點P,使d0=
在第一象限上的一個點,過點P分別作PM⊥x軸,作PN⊥y軸,記P到直線MN的距離為d0,問是否存在點P,使d0=![]() ?若存在,求出點P的坐標,若不存在,請說明理由.
?若存在,求出點P的坐標,若不存在,請說明理由.
(3)如圖3,若直線y=kx+m與拋物線y=x2﹣4x相交于x軸上方兩點A、B(A在B的左邊).且∠AOB=90°,求點P(2,0)到直線y=kx+m的距離最大時,直線y=kx+m的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
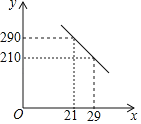
【題目】一名大學畢業生響應國家“自主創業”的號召,在成都市高新區租用了一個門店,聘請了兩名員工,計劃銷售一種產品.已知該產品成本價是20元/件,其銷售價不低于成本價,且不高于30元/件,員工每人每天的工資為200元.經過市場調查發現,該產品每天的銷售量y(件)與銷售價x(元/件)之間的函數關系如圖所示.
(1)求y與x之間的函數關系式;
(2)求每件產品銷售價為多少元時,每天門店的純利潤最大?最大純利潤是多少?(純利潤=銷售收入﹣產品成本﹣員工工資)
查看答案和解析>>
科目:初中數學 來源: 題型:
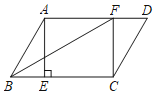
【題目】如圖,ABCD中,點E,F分別在邊BC,AD上,BE=DF,∠AEC=90°.
(1)求證:四邊形AECF是矩形;
(2)連接BF,若AB=4,∠ABC=60°,BF平分∠ABC,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC中,∠ACB=90°,AC=BC=![]() ,M為BC邊上的一個動點(不與點B,C重合),連接AM,以點A為中心,將線段AM逆時針旋轉135°,得到線段AN,連接BN.
,M為BC邊上的一個動點(不與點B,C重合),連接AM,以點A為中心,將線段AM逆時針旋轉135°,得到線段AN,連接BN.

(1)依題意補全圖2;
(2)求證:∠BAN=∠AMB;
(3)點P在線段BC的延長線上,點M關于點P的對稱點為Q,寫出一個PC的值,使得對于任意的點M,總有AQ=BN,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
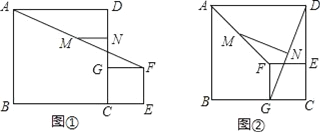
【題目】如圖①,C為線段BE上的一點,分別以BC和CE為邊在BE的同側作正方形ABCD和正方形CEFG,M、N分別是線段AF和GD的中點,連接MN
(1)線段MN和GD的數量關系是_____,位置關系是_____;
(2)將圖①中的正方形CEFG繞點C逆時針旋轉90°,其他條件不變,如圖②,(1)的結論是否成立?說明理由;
(3)已知BC=7,CE=3,將圖①中的正方形CEFG繞點C旋轉一周,其他條件不變,直接寫出MN的最大值和最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線L:y=kx+2k(k>0)與x軸交于點A,與y軸交于點B,與函數![]() (x>0)的圖象的交點P位于第一象限.
(x>0)的圖象的交點P位于第一象限.
(1)若點P的坐標為(1,6),
①求m的值及點A的坐標;
②![]() =_________;
=_________;
(2)直線h:y=2kx-2與y軸交于點C,與直線L1交于點Q,若點P的橫坐標為1,
①寫出點P的坐標(用含k的式子表示);
②當PQ≤PA時,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com