
【題目】計算: ![]() ﹣2cos30°+(
﹣2cos30°+( ![]() )﹣2﹣|1﹣
)﹣2﹣|1﹣ ![]() |.
|.
【答案】解:原式=3 ![]() ﹣2×
﹣2× ![]() +4﹣(
+4﹣( ![]() ﹣1),
﹣1),
=3 ![]() ﹣
﹣ ![]() +4﹣
+4﹣ ![]() +1,
+1,
= ![]() +5
+5
【解析】先依據算術平方根、特殊銳角三角函數值,負整數指數冪的性質,絕對值的性質進行化簡,然后再進行計算即可.
【考點精析】解答此題的關鍵在于理解整數指數冪的運算性質的相關知識,掌握aman=am+n(m、n是正整數);(am)n=amn(m、n是正整數);(ab)n=anbn(n是正整數);am/an=am-n(a不等于0,m、n為正整數);(a/b)n=an/bn(n為正整數),以及對二次根式的性質與化簡的理解,了解1、如果被開方數是分數(包括小數)或分式,先利用商的算數平方根的性質把它寫成分式的形式,然后利用分母有理化進行化簡.2、如果被開方數是整數或整式,先將他們分解因數或因式,然后把能開得盡方的因數或因式開出來.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某人去水果批發市場采購獼猴桃,他看中了A、B兩家獼猴桃.這兩家獼猴桃品質一樣,零售價都為6元/千克,批發價各不相同,
A家規定:批發數量不超過1000千克,按零售價的92%優惠;批發數量不超過2000千克,按零售價的90%優惠;超過2000千克的按零售價的88%優惠.
B家的規定如下表:
數量范圍 (千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
價格(元) | 零售價的95% | 零售價的85% | 零售價的75% | 零售價的70% |
(1)如果他批發600千克獼猴桃,則他在A 、B兩家批發分別需要多少元?
(2)如果他批發x千克獼猴桃(1500<x<2000),請你分別用含x的代數式表示他在A、B兩家批發所需的費用;
(3)現在他要批發1800千克獼猴桃,你能幫助他選擇在哪家批發更優惠嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某紙品加工廠利用邊角料裁出正方形和長方形兩種硬紙片,長方形的寬與正方形的邊長相等(如圖2),再將它們制作成甲乙兩種無蓋的長方體小盒(如圖1).現將300張長方形硬紙片和150張正方形硬紙片全部用于制作這兩種小盒,可以做成甲乙兩種小盒各多少個?(注:圖1中向上的一面無蓋)
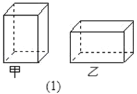
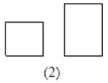
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一條直線過點(0,4),且與拋物線y= ![]() x2交于A,B兩點,其中點A的橫坐標是﹣2.
x2交于A,B兩點,其中點A的橫坐標是﹣2.
(1)求這條直線的函數關系式及點B的坐標.
(2)在x軸上是否存在點C,使得△ABC是直角三角形?若存在,求出點C的坐標,若不存在,請說明理由.
(3)過線段AB上一點P,作PM∥x軸,交拋物線于點M,點M在第一象限,點N(0,1),當點M的橫坐標為何值時,MN+3MP的長度最大?最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一天,媽媽下班后從公司開車回家,途中想起忘了帶第二天早上開早會的一個文件夾,于是打電話讓辦公室王阿姨馬上從公司送來,同時媽媽也往回開,遇到王阿姨后停下說了幾句話,接著繼續開車回家.設媽媽從公司出發后所用時間為t,媽媽與家的距離為s.下面能反映s與t的函數關系的大致圖象是( )
A.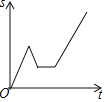 B.
B.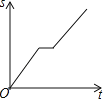
C. D.
D.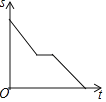
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,分別以點A和點B為圓心,大于![]() AB的長為半徑畫弧,兩弧相交于點M,N,作直線MN,交BC于點D,連接AD.若△ADC的周長為10,AB=7,則△ABC的周長為 .
AB的長為半徑畫弧,兩弧相交于點M,N,作直線MN,交BC于點D,連接AD.若△ADC的周長為10,AB=7,則△ABC的周長為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△DAC和△EBC均是等邊三角形,AE、BD分別與CD、CE交于點M、N,且A、C、B在同一直線上,有如下結論:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正確結論有( )

A. 5個 B. 4個 C. 3個 D. 2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【發現證明】如圖1,點E,F分別在正方形ABCD的邊BC,CD上,∠EAF=45°,試判斷BE,EF,FD之間的數量關系.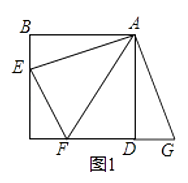
小聰把△ABE繞點A逆時針旋轉90°至△ADG,通過證明△AEF≌△AGF;從而發現并證明了EF=BE+FD.
(1)【類比引申】如圖2,點E,F分別在正方形ABCD的邊CB,CD的延長線上,∠EAF=45°,連接EF,請根據小聰的發現給你的啟示寫出EF,BE,DF之間的數量關系,并證明;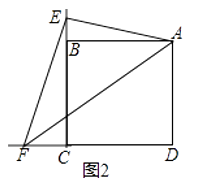
(2)【聯想拓展】如圖3,如圖,∠BAC=90°,AB=AC,點E、F在邊BC上,且∠EAF=45°,若BE=3,EF=5,求CF的長.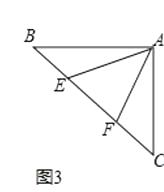
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們約定:如果身高在選定標準的±2%范圍之內都稱為“普通身高”.為了了解某校九年級男生中具有“普遍身高”的人數,我們從該校九年級男生中隨機抽出10名男生,分別測量出他們的身高(單位:cm),收集并整理如下統計表:

(1)計算這組數據的三個統計量:平均數、中位數、眾數;
(2)請你選擇其中一個統計量作為選定標準,找出這10名男生中具有“普遍身高”是哪幾位男生?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com