【題目】下列說法正確的是（ ）
A.正數和負數互為相反數
B.-a的相反數是正數
C.任何有理數的絕對值都大于它本身
D.任何一個有理數都有相反數
【答案】D
【解析】嚴格按照有理數的有關內容進行分析判斷
A、a與-a才是相反數，也就是說絕對值相等，只是符號不同的兩個數才叫互為相反數，例如2與-2等；
B、對于
， 當a=0時，=0；當a＞0時，＜0；當a＜0時，＞0；
C、設這個有理數為a，當a＜0時，
＞0＞a；當a≥0時，=a；
D、任何一個有理數都有相反數，a的相反數為-a；
綜上所述，與所給選項對比可知，A、B、C都是錯誤的，只有D是正確的。
故選D
試題
【考點精析】關于本題考查的相反數和絕對值，需要了解只有符號不同的兩個數，我們說其中一個是另一個的相反數；0的相反數還是0；相反數的和為0；a+b=0 ：a、b互為相反數；正數的絕對值是其本身，0的絕對值是0，負數的絕對值是它的相反數；注意：絕對值的意義是數軸上表示某數的點離開原點的距離才能得出正確答案．
科目：初中數學 來源： 題型：
【題目】已知AB是一段只有3米長的窄道路，由于一輛小汽車與一輛大卡車在AB段相遇，必須倒車才能繼續通過．如果小汽車在AB段正常行駛需10分鐘，大卡車在AB段正常行駛需20分鐘，小汽車在AB段倒車的速度是它正常行駛速度的
，大卡車在AB段倒車的速度是它正常行駛的
，小汽車需倒車的路程是大卡車的4倍．問兩車都通過AB這段狹窄路面的最短時間是 分鐘．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠C=90°，AC=6，BC=8，點F在邊AC上，并且CF=2，點E為邊BC上的動點，將△CEF沿直線EF翻折，點C落在點P處，則點P到邊AB距離的最小值是 ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算:
(1) (－4x2y)·(－x2y2)·(
y)3； (2) (－3ab)(2a2b＋ab－1) ；
(3) (m－
)(m＋
)； （4） （-x-1）(-x+1) ； (5) ( - x - 5)2 ； （6）
；
（7）先化簡，再求值：（x+1）2﹣（x+2）（x﹣2），其中
；
(8)解方程組
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】特值驗證：
當
，0，1，2，5，…時，計算代數式
的值，分別得到5，2，1，2，17，…．當x的取值發生變化時，代數式的值卻有一個確定的范圍，通過多次驗證可以發現它的值總大于或等于1，所以1就是它的最小值．
變式求證：
我們可以用學過的知識，對進行恒等變形：
．（注：這種變形方法可稱為“配方”） 
，
．所以無論x取何值，代數式的值不小于1，即最小值為1．
遷移實證：
（1）請你用“配方”的方法，確定
的最小值為3；
（2）求
的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知點P是直線
上一定點，點A是x軸上一動點
不與原點重合
，連接PA，過點P作
，交y軸于點B，探究線段PA與PB的數量關系．
1
如圖
，當
軸時，觀察圖形發現線段PA與PB的數量關系是______；
2
當PA與x軸不垂直時，在圖
中畫出圖形，線段PA與PB的數量關系是否與
Ⅰ
所得結果相同？寫出你的猜想并加以證明；
3 
為何值時，線段
？此時
的度數是多少，為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司在
兩倉庫分別有機器16臺和12臺，現要運往甲、乙兩地，其中甲地需要15臺，乙地需要13臺，已知
兩地倉庫運往甲，乙兩地機器的費用如下面的左表所示．
設從A倉庫調x臺機器去甲地，請用含x的代數式補全下面的右表；
機器調運費用表機器調運方案表
出發地 目的地運費 | A | B | 出發地 目的地機器 | A | B | 合計 | |
甲 | 500 | 300 | 甲地 | x | 15 | ||
乙 | 400 | 600 | 乙地 | 13 | |||
合計 | 16 | 12 | 28 |
設總運費為y元，求y與x之間的函數解析式，并寫出自變量x的取值范圍；
由機器調運方案表可知共有n種調運方案，求n的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在
中， 
， 
，點
在
的延長線上， 
是
的中點， 
是射線
上一動點，且
，連接
，作
， 
交
延長線于點
．
（
）如圖
，當點
在
上時，填空： 
__________ 
（填“
”、“
”或“
”）．
（
）如圖
，當點
在
的延長線上時，請根據題意將圖形補全，判斷
與
的數量關系，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
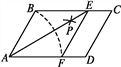
【題目】如圖,在ABCD中,以點A為圓心,AB長為半徑畫弧交AD于點F,再分別以點B,F為圓心,大于BF的相同長為半徑畫弧,兩弧交于點P;連接AP并延長交BC于點E,連接EF,則所得四邊形ABEF是菱形.
(1)根據以上尺規作圖的過程,求證:四邊形ABEF是菱形;
(2)若菱形ABEF的周長為16,AE=
,求∠C的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
