
【題目】某服裝廠(chǎng)每天生產(chǎn)![]() 、
、![]() 兩種品牌的服裝共600件,
兩種品牌的服裝共600件,![]() 、
、![]() 兩種品牌的服裝每件的成本和利潤(rùn)如右表:
兩種品牌的服裝每件的成本和利潤(rùn)如右表:
A | B | |
成本(元/件) | 50 | 35 |
利潤(rùn)(元/件) | 20 | 15 |
設(shè)每天生產(chǎn)![]() 種品牌服裝
種品牌服裝![]() 件,每天兩種服裝獲利
件,每天兩種服裝獲利![]() 元.
元.
(1)請(qǐng)寫(xiě)出![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)如果服裝廠(chǎng)每天至少投入成本26400元,那么每天至少獲利多少元?
【答案】(1) ![]() (2)
(2) ![]() ,
,![]()
【解析】分析:(1)根據(jù)總利潤(rùn)=A品牌的利潤(rùn)+B品牌的利潤(rùn)列方程;(2)A品牌的成本+B品牌的成本≥26400列不等式,求出x的最小值,結(jié)合(1)求解.
詳解:(1)根據(jù)題意得,y=20x+15(600-x),
即y=5x+9000.
(2)根據(jù)題意得,50x+35(600-x)≥26400,
解得x≥360,
當(dāng)x取最小值360時(shí)利潤(rùn)y有最小值5×360+9000=10800元.
答:每天至少獲利10800元.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知正方形ABCD,點(diǎn)E是BC邊的中點(diǎn),DE與AC相交于點(diǎn)F,連接BF,下列結(jié)論:①S△ABF=S△ADF②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正確的是( )
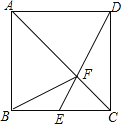
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知線(xiàn)段![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 是
是![]() 的中點(diǎn).
的中點(diǎn).
![]()
(1)若![]() ,求線(xiàn)段
,求線(xiàn)段![]() 的長(zhǎng)度.
的長(zhǎng)度.
(2)當(dāng)線(xiàn)段![]() 在線(xiàn)段
在線(xiàn)段![]() 上從左向右或從右向左運(yùn)動(dòng)時(shí),試判斷線(xiàn)段
上從左向右或從右向左運(yùn)動(dòng)時(shí),試判斷線(xiàn)段![]() 的長(zhǎng)度是否發(fā)生變化,如果不變,請(qǐng)求出線(xiàn)段
的長(zhǎng)度是否發(fā)生變化,如果不變,請(qǐng)求出線(xiàn)段![]() 的長(zhǎng)度;如果變化,請(qǐng)說(shuō)明理由.
的長(zhǎng)度;如果變化,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】我們定義:如圖1,在△ABC看,把AB點(diǎn)繞點(diǎn)A順時(shí)針旋轉(zhuǎn)α(0°<α<180°)得到AB',把AC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)β得到AC',連接B'C'.當(dāng)α+β=180°時(shí),我們稱(chēng)△A'B'C'是△ABC的“旋補(bǔ)三角形”,△AB'C'邊B'C'上的中線(xiàn)AD叫做△ABC的“旋補(bǔ)中線(xiàn)”,點(diǎn)A叫做“旋補(bǔ)中心”.
特例感知:
(1)在圖2,圖3中,△AB'C'是△ABC的“旋補(bǔ)三角形”,AD是△ABC的“旋補(bǔ)中線(xiàn)”.
①如圖2,當(dāng)△ABC為等邊三角形時(shí),AD與BC的數(shù)量關(guān)系為AD= BC;
②如圖3,當(dāng)∠BAC=90°,BC=8時(shí),則AD長(zhǎng)為 .
猜想論證:
(2)在圖1中,當(dāng)△ABC為任意三角形時(shí),猜想AD與BC的數(shù)量關(guān)系,并給予證明.
拓展應(yīng)用
(3)如圖4,在四邊形ABCD,∠C=90°,∠D=150°,BC=12,CD=2![]() ,DA=6.在四邊形內(nèi)部是否存在點(diǎn)P,使△PDC是△PAB的“旋補(bǔ)三角形”?若存在,給予證明,并求△PAB的“旋補(bǔ)中線(xiàn)”長(zhǎng);若不存在,說(shuō)明理由.
,DA=6.在四邊形內(nèi)部是否存在點(diǎn)P,使△PDC是△PAB的“旋補(bǔ)三角形”?若存在,給予證明,并求△PAB的“旋補(bǔ)中線(xiàn)”長(zhǎng);若不存在,說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:若a+b=ab,則稱(chēng)a、b是“相伴數(shù)”,例如:3+1.5=3×1.5,因此3和1.5是一組“相伴數(shù)”
(1)﹣1與 是一組“相伴數(shù)”;
(2)若m、n是一組“相伴數(shù)”,2mn﹣![]() [3m+2(
[3m+2(![]() n﹣m)+3mn﹣6]的值.
n﹣m)+3mn﹣6]的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,AD是∠BAC的平分線(xiàn),AD的垂直平分線(xiàn)交BC的延長(zhǎng)線(xiàn)于點(diǎn)F.
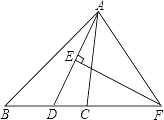
(1)求證:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在每個(gè)小正方形邊長(zhǎng)為1的網(wǎng)格中,點(diǎn)A,B,C均在格點(diǎn)上.
(Ⅰ)AC的長(zhǎng)度等于_____;
(Ⅱ)在圖中有一點(diǎn)P,若連接AP,PB,PC,滿(mǎn)足AP平分∠A,且PC=PB,請(qǐng)?jiān)谌鐖D所示的網(wǎng)格中,用無(wú)刻度的直尺,畫(huà)出點(diǎn)P,并簡(jiǎn)要說(shuō)明點(diǎn)P的位置是如何找到的(不要求證明)_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】將一副三角板的兩個(gè)銳角頂點(diǎn)重合,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的平分線(xiàn).
的平分線(xiàn).
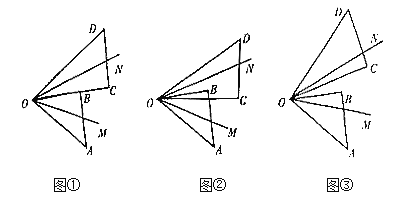
(1)如圖①所示,當(dāng)![]() 與
與![]() 重合時(shí),則
重合時(shí),則![]() 的大小為______.
的大小為______.
(2)當(dāng)![]() 繞著點(diǎn)
繞著點(diǎn)![]() 旋轉(zhuǎn)至如圖②所示,當(dāng)
旋轉(zhuǎn)至如圖②所示,當(dāng)![]() ,則
,則![]() 的大小為多少?
的大小為多少?
(3)當(dāng)![]() 繞著點(diǎn)
繞著點(diǎn)![]() 旋轉(zhuǎn)至如圖③所示,當(dāng)
旋轉(zhuǎn)至如圖③所示,當(dāng)![]() 時(shí),求
時(shí),求![]() 的大小.
的大小.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com