
【題目】(1)如圖1,在![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞頂點(diǎn)
繞頂點(diǎn)![]() 逆時針旋轉(zhuǎn)時,當(dāng)
逆時針旋轉(zhuǎn)時,當(dāng)![]() 時,設(shè)
時,設(shè)![]() 與
與![]() 于
于![]() ,證明:
,證明:![]() 是等邊三角形;
是等邊三角形;
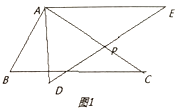
(2)如圖1,在![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞頂點(diǎn)
繞頂點(diǎn)![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 多少度時,
多少度時,![]() ,使得
,使得![]() 的頂點(diǎn)
的頂點(diǎn)![]() 落在
落在![]() 上?
上?
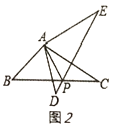
(3)當(dāng)直角三角形變?yōu)橐话闳切螘r,如圖2,將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得到
得到![]() ,
,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,可以得到
,可以得到![]() ,試證明:
,試證明:![]() .
.
【答案】(1)詳見解析;(2)![]() ;(3)詳見解析.
;(3)詳見解析.
【解析】
(1)由![]() ,
,![]() 得∠CBA=60°,根據(jù)旋轉(zhuǎn)的性質(zhì)可得∠AED=∠ACB=30°,而
得∠CBA=60°,根據(jù)旋轉(zhuǎn)的性質(zhì)可得∠AED=∠ACB=30°,而![]() ,所以∠ACB=∠CAE =30°,再根據(jù)三角形內(nèi)角和定理即可解答;
,所以∠ACB=∠CAE =30°,再根據(jù)三角形內(nèi)角和定理即可解答;
(2) 先計算∠B=60°,根據(jù)旋轉(zhuǎn)性質(zhì)得AB=AD,可知△ABD是等邊三角形,則旋轉(zhuǎn)角∠BAD的度數(shù)可求.
(3)連接![]() ,延長
,延長![]() 到
到![]() ,使
,使![]() ,連接
,連接![]() ,利用旋轉(zhuǎn)的性質(zhì)得到
,利用旋轉(zhuǎn)的性質(zhì)得到![]() 是等邊三角形,再根據(jù)等邊三角形的性質(zhì)證明
是等邊三角形,再根據(jù)等邊三角形的性質(zhì)證明![]() ,即可解答.
,即可解答.
如圖1,∵在△ABC中,![]() ,
,![]() ,
,
∴∠CBA=60°(直角三角形的兩個銳角互余).
∵![]() ,
,
∴∠ACB=∠CAE,
又由旋轉(zhuǎn)的性質(zhì)知,∠AED=∠ACB=30°,
∴∠ACB=∠CAE =30°,
∴∠PAD=∠EAD-CAE =90°-30°=60°,
∴∠ADP=60°,
∴在△CDB中,∠ADP =∠PAD =60°,
∴∠APD=180°-60°-60°=60°,
∴△ADP是等邊三角形;
(2)∵∠BAC=90°,∠ACB=30°,
∴∠B=60°.
根據(jù)旋轉(zhuǎn)的性質(zhì)可知AB=AD,
∴△ABD是等邊三角形,
旋轉(zhuǎn)角∠BAD=60°.
故答案為60°.
(3)證明:連接![]() ,延長
,延長![]() 到
到![]() ,使
,使![]() ,連接
,連接![]() ,
,
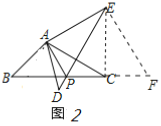
由旋轉(zhuǎn)可知:∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,
∵![]() ,∴
,∴![]()
在![]() 和
和![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
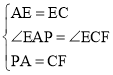
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() 為
為![]() 邊上一點(diǎn).
邊上一點(diǎn).
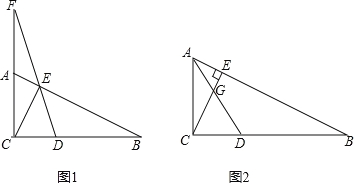
(1)當(dāng)![]() 時,直接寫出
時,直接寫出![]() ,
,![]() .
.
(2)如圖1,當(dāng)![]() ,
,![]() 時,連
時,連![]() 并延長交
并延長交![]() 延長線于
延長線于![]() ,求證:
,求證:![]() .
.
(3)如圖2,連![]() 交
交![]() 于
于![]() ,當(dāng)
,當(dāng)![]() 且
且![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將邊長為2cm的正方形OABC放在平面直角坐標(biāo)系中,O是原點(diǎn),點(diǎn)A的橫坐標(biāo)為1,則點(diǎn)C的坐標(biāo)為( )
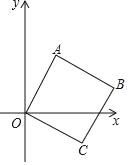
A. (![]() ,-1) B. (2,﹣1) C. (1,-
,-1) B. (2,﹣1) C. (1,-![]() ) D. (﹣1,
) D. (﹣1,![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校門口豎著“前方學(xué)校,減速慢行”的交通指示牌CD,數(shù)學(xué)“綜合與實(shí)踐”小組的同學(xué)將“測量交通指示牌CD的高度”作為一項課題活動,他們定好了如下測量方案:
項目 | 內(nèi)容 |
課題 | 測量交通指示牌CD的高度 |
測量示意圖 |
|
測量步驟 | (1)從交通指示牌下的點(diǎn)M處出發(fā)向前走10 米到達(dá)A處; (2)在點(diǎn)A處用量角儀測得∠DAM=27°; (3)從點(diǎn)A沿直線MA向前走10米到達(dá)B處;(4)在點(diǎn)B處用量角儀測得∠CBA=18°. |
請你幫助該小組同學(xué)根據(jù)上表中的測量數(shù)據(jù),求出交通指示牌CD的高度.(參考數(shù)據(jù)sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知關(guān)于x的一元二次方程![]() 。
。
(1)求證:方程有兩個不相等的實(shí)數(shù)根;
(2)若△ABC的兩邊AB、AC的長是方程的兩個實(shí)數(shù)根,第三邊BC的長為5。當(dāng)△ABC是等腰三角形時,求k的值。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】用黑白棋子擺出下列一組圖形,根據(jù)規(guī)律可知.
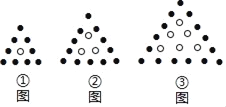
(1)在第n個圖中,白棋共有 枚,黑棋共有 枚;
(2)在第幾個圖形中,白棋共有300枚;
(3)白棋的個數(shù)能否與黑棋的個數(shù)相等?若能,求出是第幾個圖形,若不能,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩車間同時開始加工一批服裝.從開始加工到加工完這批服裝甲車間工作了9小時,乙車間在中途停工一段時間維修設(shè)備,然后按停工前的工作效率繼續(xù)加工,直到與甲車間同時完成這批服裝的加工任務(wù)為止.設(shè)甲、乙兩車間各自加工服裝的數(shù)量為y(件).甲車間加工的時間為x(時),y與x之間的函數(shù)圖象如圖所示,則下列結(jié)論錯誤的是( )
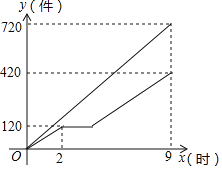
A.甲車間每小時加工服裝80件
B.這批服裝的總件數(shù)為1140件
C.乙車間每小時加工服裝為60件
D.乙車間維修設(shè)備用了4小時
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
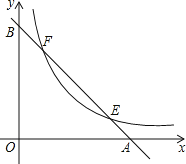
【題目】如圖,已知直線y=﹣x+2分別與x軸,y軸交于A,B兩點(diǎn),與雙曲線y=![]() 交于E,F兩點(diǎn),若AB=2EF,則k的值是_____.
交于E,F兩點(diǎn),若AB=2EF,則k的值是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,是二次函數(shù)y=ax2+bx+c(a≠0)的圖象,對稱軸為直線x=2,則下列結(jié)論正確的有( )個.
①ax2+bx+c=0(a≠0)有兩個不相等的實(shí)數(shù)根
②3a﹣c>0
③a﹣b+c<0
④(0,y1)、(4,y2)在此二次函數(shù)的圖象上,則y1<y2
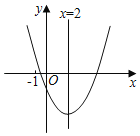
A.1B.2C.3D.4
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com