
【題目】如圖,在平面直角坐標(biāo)系中,將坐標(biāo)原點![]() 沿
沿![]() 軸向左平移
軸向左平移![]() 個單位長度得到點
個單位長度得到點![]() ,過點
,過點![]() 作
作![]() 軸的平行線交反比例函數(shù)
軸的平行線交反比例函數(shù)![]() 的圖象于點
的圖象于點![]() ,
,![]() .
.
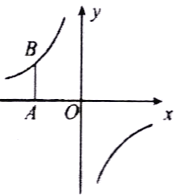
(1)求反比例函數(shù)的解析式;
(2)若![]() 、
、![]() 是該反比例函數(shù)圖象上的兩點,且當(dāng)
是該反比例函數(shù)圖象上的兩點,且當(dāng)![]() 時,
時,![]() ,指出點
,指出點![]() 、
、![]() 各位于哪個象限?并簡要說明理由.
各位于哪個象限?并簡要說明理由.
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知動點A在函數(shù)![]() 的圖象上,AB⊥x軸于點B,AC⊥y軸于點C,延長CA交以A為圓心AB長為半徑的圓弧于點E,延長BA交以A為圓心AC長為半徑的圓弧于點F,直線EF分別交x軸、y軸于點M、N,當(dāng)NF=4EM時,圖中陰影部分的面積等于_____.
的圖象上,AB⊥x軸于點B,AC⊥y軸于點C,延長CA交以A為圓心AB長為半徑的圓弧于點E,延長BA交以A為圓心AC長為半徑的圓弧于點F,直線EF分別交x軸、y軸于點M、N,當(dāng)NF=4EM時,圖中陰影部分的面積等于_____.
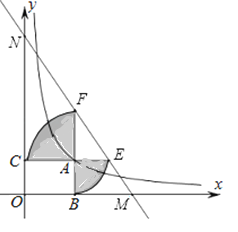
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(問題原型)如圖,在![]() 中,對角線
中,對角線![]() 的垂直平分線
的垂直平分線![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .求證:四邊形
.求證:四邊形![]() 是菱形.
是菱形.

(小海的證法)證明:
![]()
![]() 是
是![]() 的垂直平分線,
的垂直平分線,
![]()
![]() ,(第一步)
,(第一步)
![]() ,(第二步)
,(第二步)
![]() .(第三步)
.(第三步)
![]() 四邊形
四邊形![]() 是平行四邊形.(第四步)
是平行四邊形.(第四步)
![]() 四邊形
四邊形![]() 是菱形. (第五步)
是菱形. (第五步)
(老師評析)小海利用對角線互相平分證明了四邊形![]() 是平行四邊形,再利用對角線互相垂直證明它是菱形,可惜有一步錯了.
是平行四邊形,再利用對角線互相垂直證明它是菱形,可惜有一步錯了.
(挑錯改錯)(1)小海的證明過程在第________步上開始出現(xiàn)了錯誤.
(2)請你根據(jù)小海的證題思路寫出此題的正確解答過程,
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1和2,![]() 中,AB=3,BC=15,
中,AB=3,BC=15,![]() .點
.點![]() 為
為![]() 延長線上一點,過點
延長線上一點,過點![]() 作
作![]() 切
切![]() 于點
于點![]() ,設(shè)
,設(shè)![]() .
.
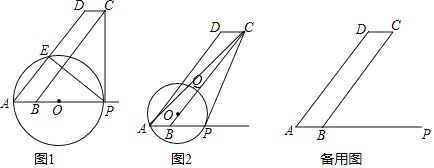
(1)如圖1,![]() 為何值時,圓心
為何值時,圓心![]() 落在
落在![]() 上?若此時
上?若此時![]() 交
交![]() 于點
于點![]() ,直接指出PE與BC的位置關(guān)系;
,直接指出PE與BC的位置關(guān)系;
(2)當(dāng)![]() 時,如圖2,
時,如圖2,![]() 與
與![]() 交于點
交于點![]() ,求
,求![]() 的度數(shù),并通過計算比較弦
的度數(shù),并通過計算比較弦![]() 與劣弧
與劣弧![]() 長度的大小;
長度的大小;
(3)當(dāng)![]() 與線段
與線段![]() 只有一個公共點時,直接寫出
只有一個公共點時,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)y= ax2 + bx +c經(jīng)過點A(-1,0), B(3,0), C(0,-3).
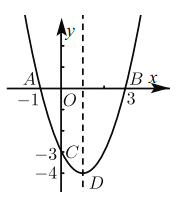
(1)求該二次函數(shù)的解析式.
(2)利用圖象的特點填空.
①當(dāng)x= ___ 時方程ax2 + bx+c=-3.
當(dāng)x= ___時方程ax2 +bx+c=-4.
②不等式ax2 + bx + c> 0的解集為
不等式-4<ax2+bx+c<0的解集為.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】勝利中學(xué)為豐富同學(xué)們的校園生活,舉行“校園電視臺主待人”選拔賽,現(xiàn)將36名參賽選手的成績(單位:分)統(tǒng)計并繪制成頻數(shù)分布直方圖和扇形統(tǒng)計圖,部分信息如下:
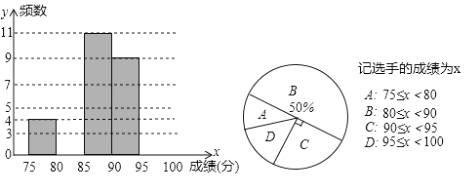
請根據(jù)統(tǒng)計圖的信息,解答下列問題:
(1)補全頻數(shù)分布直方圖,并求扇形統(tǒng)計圖中扇形![]() 對應(yīng)的圓心角度數(shù);
對應(yīng)的圓心角度數(shù);
(2)成績在![]() 區(qū)域的選手,男生比女生多一人,從中隨機抽取兩人臨時擔(dān)任該校藝術(shù)節(jié)的主持人,求恰好選中一名男生和一名女生的概率.
區(qū)域的選手,男生比女生多一人,從中隨機抽取兩人臨時擔(dān)任該校藝術(shù)節(jié)的主持人,求恰好選中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商店銷售一種商品,童威經(jīng)市場調(diào)查發(fā)現(xiàn):該商品的周銷售量![]() (件)是售價
(件)是售價![]() (元/件)的一次函數(shù),其售價、周銷售量、周銷售利潤
(元/件)的一次函數(shù),其售價、周銷售量、周銷售利潤![]() (元)的三組對應(yīng)值如下表:
(元)的三組對應(yīng)值如下表:
售價 | 50 | 60 | 80 |
周銷售量 | 100 | 80 | 40 |
周銷售利潤 | 1000 | 1600 | 1600 |
注:周銷售利潤=周銷售量×(售價-進(jìn)價)
(1)①求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式(不要求寫出自變量的取值范圍)
的函數(shù)解析式(不要求寫出自變量的取值范圍)
②該商品進(jìn)價是_________元/件;當(dāng)售價是________元/件時,周銷售利潤最大,最大利潤是__________元
(2)由于某種原因,該商品進(jìn)價提高了![]() 元/件
元/件![]() ,物價部門規(guī)定該商品售價不得超過65元/件,該商店在今后的銷售中,周銷售量與售價仍然滿足(1)中的函數(shù)關(guān)系.若周銷售最大利潤是1400元,求
,物價部門規(guī)定該商品售價不得超過65元/件,該商店在今后的銷售中,周銷售量與售價仍然滿足(1)中的函數(shù)關(guān)系.若周銷售最大利潤是1400元,求![]() 的值
的值
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,拋物線y=ax2+bx+c的頂點坐標(biāo)為P(2,9),與x軸交于點A,B,與y軸交于點C(0,5).
(Ⅰ)求二次函數(shù)的解析式及點A,B的坐標(biāo);
(Ⅱ)設(shè)點Q在第一象限的拋物線上,若其關(guān)于原點的對稱點Q′也在拋物線上,求點Q的坐標(biāo);
(Ⅲ)若點M在拋物線上,點N在拋物線的對稱軸上,使得以A,C,M,N為頂點的四邊形是平行四邊形,且AC為其一邊,求點M,N的坐標(biāo).

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com