
【題目】如圖,E是平行四邊形ABCD的邊CD的中點,延長AE交BC的延長線于點F.
(1)求證:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求平行四邊形ABCD的面積.

【答案】(1)見解析;(2) 24
【解析】
(1) 根據四邊形ABCD是平行四邊形,得到∠DAE=∠F,∠D=∠ECF,再根據E是平行四邊形ABCD的邊CD的中點,便可以證明出全等了.
(2) 由全等的性質,便可得到AE=EF=3,計算出DE的長度,最后計算CD即可.
(1)證明:∵四邊形ABCD是平行四邊形,∴AD∥BC,AB∥CD,∴∠DAE=∠F,∠D=∠ECF,
∵E是平行四邊形ABCD的邊CD的中點,∴DE=CE,
在△ADE和△FCE中,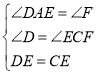 ,∴△ADE≌△FCE(AAS);
,∴△ADE≌△FCE(AAS);
(2)解:∵ADE≌△FCE,∴AE=EF=3,∵AB∥CD,∴∠AED=∠BAF=90°,
在平行四邊形ABCD中,AD=BC=5,∴DE=![]() =4,∴CD=2DE=8.
=4,∴CD=2DE=8.
∴平行四邊形ABCD的面積是:8×3=24.


科目:初中數學 來源: 題型:
【題目】如圖,矩形DEFG的邊EF在△ABC的邊BC上,頂點D,G分別在邊AB,AC上,AH⊥BC,垂足為H,AH交DG于點P,已知BC=6,AH=4.當矩形DEFG面積最大時,HP的長是( )
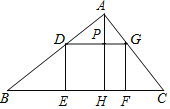
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在抗疫期間,藥店銷售![]() 兩種類型的口罩,已知銷售
兩種類型的口罩,已知銷售![]() 只
只![]() 型口罩和
型口罩和![]() 只
只![]() 型口罩的潤為
型口罩的潤為![]() 元,售
元,售![]() 只
只![]() 型口罩和
型口罩和![]() 只
只![]() 型口罩的利潤為
型口罩的利潤為![]() 元,
元,
(1)每只![]() 型口罩和
型口罩和![]() 型口罩的利潤;
型口罩的利潤;
(2)該藥店計劃一次購進兩種型號的口罩![]() 只,其中
只,其中![]() 型口罩的進貨量不超過
型口罩的進貨量不超過![]() 型口罩的
型口罩的![]() 倍,設購進
倍,設購進![]() 型
型![]() 罩
罩![]() 只,這
只,這![]() 口罩的利潤為
口罩的利潤為![]() 元;
元;
①求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
②藥店購進![]() 型口各多少才能使銷售總利潤最大?
型口各多少才能使銷售總利潤最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() ,
,![]() ,過點
,過點![]() 作直線
作直線![]() ,
,
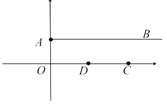
(1)若![]() ,點
,點![]() 是線段
是線段![]() 的中點,點
的中點,點![]() 在射線
在射線![]() 上,當
上,當![]() 是邊長為5的等腰三角形,共有幾個這樣的點
是邊長為5的等腰三角形,共有幾個這樣的點![]() ,并嘗試求出點
,并嘗試求出點![]() 的坐標;
的坐標;
(2)若直線![]() 與
與![]() 不平行,
不平行,![]() 在直線
在直線![]() 上,是否存在點
上,是否存在點![]() ,使得
,使得![]() 是直角三角形,且
是直角三角形,且![]() ,若存在,求出這樣的點
,若存在,求出這樣的點![]() 坐標;若不存在,請說明理由.
坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】發現任意三個連續的整數中,最大數與最小數這兩個數的平方差是4的倍數;
驗證:(1) ![]() 的結果是4的幾倍?
的結果是4的幾倍?
(2)設三個連續的整數中間的一個為n,計算最大數與最小數這兩個數的平方差,并說明它是4的倍數;
延伸:說明任意三個連續的奇數中,最大的數與最小的數這兩個數的平方差是8的倍數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,點E,F分別是AD,BC的中點,G,H分別是BD,AC的中點,AB,CD滿足( )條件時,四邊形EGFH是菱形.
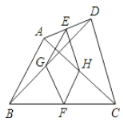
A.AB=CDB.AB//CDC.AB⊥CDD.AB=CD AB//CD
查看答案和解析>>
科目:初中數學 來源: 題型:
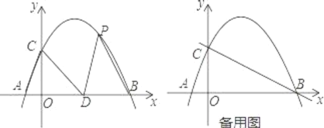
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+2經過點A(﹣1,0)和點B(4,0),且與y軸交于點C,點D的坐標為(2,0),點P(m,n)是該拋物線上的一個動點,連接CA,CD,PD,PB.
(1)求該拋物線的解析式;
(2)當△PDB的面積等于△CAD的面積時,求點P的坐標;
(3)當m>0,n>0時,過點P作直線PE⊥y軸于點E交直線BC于點F,過點F作FG⊥x軸于點G,連接EG,請直接寫出隨著點P的運動,線段EG的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級(1)班全班50名同學組成五個不同的興趣愛好小組,每人都參加且只能參加一個小組,統計(不完全)人數如下表:
編號 | 一 | 二 | 三 | 四 | 五 |
人數 |
| 15 | 20 | 10 |
|
已知前面兩個小組的人數之比是![]() .
.
解答下列問題:
(1)![]() .
.
(2)補全條形統計圖:
(3)若從第一組和第五組中任選兩名同學,求這兩名同學是同一組的概率.(用樹狀圖或列表把所有可能都列出來)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com