
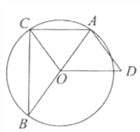
【題目】如圖,已知△ABC內接于![]() ,AB是直徑,OD∥AC,AD=OC.
,AB是直徑,OD∥AC,AD=OC.
(1)求證:四邊形OCAD是平行四邊形;
(2)填空:①當∠B= 時,四邊形OCAD是菱形;
②當∠B= 時,AD與![]() 相切.
相切.
【答案】(1)證明見解析;(2)① 30°,② 45°
【解析】試題分析:(1)根據(jù)已知條件求得∠OAC=∠OCA,∠AOD=∠ADO,然后根據(jù)三角形內角和定理得出∠AOC=∠OAD,從而證得OC∥AD,即可證得結論;
(2)①若四邊形OCAD是菱形,則OC=AC,從而證得OC=OA=AC,得出∠![]() 即可求得
即可求得![]()
②AD與![]() 相切,根據(jù)切線的性質得出
相切,根據(jù)切線的性質得出![]() 根據(jù)AD∥OC,內錯角相等得出
根據(jù)AD∥OC,內錯角相等得出![]() 從而求得
從而求得![]()
試題解析:(方法不唯一)
(1)∵OA=OC,AD=OC,
∴OA=AD,
∴∠OAC=∠OCA,∠AOD=∠ADO,
∵OD∥AC,
∴∠OAC=∠AOD,
∴∠OAC=∠OCA=∠AOD=∠ADO,
∴∠AOC=∠OAD,
∴OC∥AD,
∴四邊形OCAD是平行四邊形;
(2)①∵四邊形OCAD是菱形,
∴OC=AC,
又∵OC=OA,
∴OC=OA=AC,
∴![]()
∴![]()
故答案為: ![]()
②∵AD與![]() 相切,
相切,
∴![]()
∵AD∥OC,
∴![]()
∴![]()
故答案為: ![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:
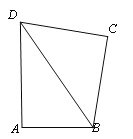
【題目】如圖,在四邊形ABCD中,AB=1,AD=![]() ,BD=2,∠ABC+∠ADC=180°,CD=
,BD=2,∠ABC+∠ADC=180°,CD=![]() .
.
(1)判斷△ABD的形狀,并說明理由;
(2)求BC的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖(1),在四邊形![]() 中,
中,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發(fā),沿
出發(fā),沿![]() ,
,![]() 運動至點
運動至點![]() 停止.設點
停止.設點![]() 運動的路程為
運動的路程為![]() ,
,![]() 的面積為
的面積為![]() ,如果
,如果![]() 關于
關于![]() 的函數(shù)圖象如圖(2)所示,則
的函數(shù)圖象如圖(2)所示,則![]() 的面積是( )
的面積是( )

A.6B.5C.4D.3
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了提高學生書寫漢字的能力,增強保護漢子的意識,某校舉辦了首屆“漢字聽寫大賽”,學生經(jīng)選拔后進入決賽,測試同時聽寫100個漢字,每正確聽寫出一個漢字得1分,本次決賽,學生成績?yōu)?/span>![]() (分),且
(分),且![]() ,將其按分數(shù)段分為五組,繪制出以下不完整表格:
,將其按分數(shù)段分為五組,繪制出以下不完整表格:
組別 | 成績 | 頻數(shù)(人數(shù)) | 頻率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
請根據(jù)表格提供的信息,解答以下問題:
(1)本次決賽共有 名學生參加;
(2)直接寫出表中a= ,b= ;
(3)請補全下面相應的頻數(shù)分布直方圖;

(4)若決賽成績不低于80分為優(yōu)秀,則本次大賽的優(yōu)秀率為 。
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于點D,PE⊥OB于點E.如果點M是OP的中點,則DM的長是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,在四邊形ABCD中,AB=AD. ∠B+∠ADC=180°,點E,F(xiàn)分別在四邊形ABCD的邊BC,CD上,∠EAF=![]() ∠BAD,連接EF,試猜想EF,BE,DF之間的數(shù)量關系.
∠BAD,連接EF,試猜想EF,BE,DF之間的數(shù)量關系.

圖1 圖2 圖3
(1)思路梳理
將△ABE繞點A逆時針旋轉至△ADG,使AB與AD重合.由∠B+∠ADC=180°,得∠FDG=180°,即點F,D,G三點共線. 易證△AFG![]() ,故EF,BE,DF之間的數(shù)量關系為 ;
,故EF,BE,DF之間的數(shù)量關系為 ;
(2)類比引申
如圖2,在圖1的條件下,若點E,F(xiàn)由原來的位置分別變到四邊形ABCD的邊CB,DC的延長線上,∠EAF=![]() ∠BAD,連接EF,試猜想EF,BE,DF之間的數(shù)量關系,并給出證明.
∠BAD,連接EF,試猜想EF,BE,DF之間的數(shù)量關系,并給出證明.
(3)聯(lián)想拓展
如圖3,在△ABC中,∠BAC=90°,AB=AC,點D,E均在邊BC上,且∠DAE=45°. 若BD=1,EC=2,則DE的長為 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知![]() ≌
≌![]() ,且
,且![]() 、
、![]() 、
、![]() 、
、![]() 四點在同一直線上.
四點在同一直線上.
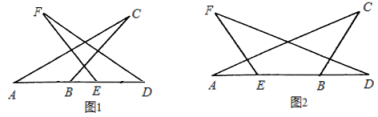
(1)在圖1中,請你用無刻度的直尺作出線段![]() 的垂直平分線;
的垂直平分線;
(2)在圖2中,請你用無刻度的直尺作出線段![]() 的垂直平分線.
的垂直平分線.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,已知![]() 中,
中,![]() 厘米,
厘米,![]() 、
、![]() 分別從點
分別從點![]() 、點
、點![]() 同時出發(fā),沿三角形的邊運動,已知點
同時出發(fā),沿三角形的邊運動,已知點![]() 的速度是1厘米/秒的速度,點
的速度是1厘米/秒的速度,點![]() 的速度是2厘米/秒,當點
的速度是2厘米/秒,當點![]() 第一次到達
第一次到達![]() 點時,
點時,![]() 、
、![]() 同時停止運動.
同時停止運動.
(1)![]() 、
、![]() 同時運動幾秒后,
同時運動幾秒后,![]() 、
、![]() 兩點重合?
兩點重合?
(2)![]() 、
、![]() 同時運動幾秒后,可得等邊三角形
同時運動幾秒后,可得等邊三角形![]() ?
?
(3)![]() 、
、![]() 在
在![]() 邊上運動時,能否得到以
邊上運動時,能否得到以![]() 為底邊的等腰
為底邊的等腰![]() ,如果存在,請求出此時
,如果存在,請求出此時![]() 、
、![]() 運動的時間?
運動的時間?

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]() 有兩個實數(shù)根.
有兩個實數(shù)根.
![]() 若
若![]() 為正整數(shù),求此方程的根.
為正整數(shù),求此方程的根.
![]() 設此方程的兩個實數(shù)根為
設此方程的兩個實數(shù)根為![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com