
【題目】常常聽說“勾3股4弦5”,是什么意思呢?它就是勾股定理,即“直角三角形兩直角邊長a,b與斜邊長c之間滿足等式:a2+b2=c2”的一個最簡單特例.我們把滿足a2+b2=c2的三個正整數a,b,c,稱為勾股數組,記為(a,b,c).
(1)請在下面的勾股數組表中寫出m、n、p合適的數值:
a | b | c | a | b | c |
3 | 4 | 5 | 4 | 3 | 5 |
5 | 12 | m | 6 | 8 | 10 |
7 | 24 | 25 | p | 15 | 17 |
9 | n | 41 | 10 | 24 | 26 |
11 | 60 | 61 | 12 | 35 | 37 |
… | … | … | … | … | … |
平面直角坐標系中,橫、縱坐標均為整數的點叫做整點(格點).過x軸上的整點作y軸的平行線,過y軸上的整點作x軸的平行線,組成的圖形叫做正方形網格(有時簡稱網格),這些平行線叫做格邊,當一條線段AB的兩端點是格邊上的點時,稱為AB在格邊上.頂點均在格點上的多邊形叫做格點多邊形.在正方形網格中,我們可以利用勾股定理研究關于圖形面積、周長的問題,其中利用割補法、作圖法求面積非常有趣.
(2)已知△ABC三邊長度為4、13、15,請在下面的網格中畫出格點△ABC并計算其面積.

科目:初中數學 來源: 題型:
【題目】在矩形ABCD中,AB=3,BC=4,E,F是對角線AC上的兩個動點,分別從A,C同時出發相向而行,速度均為1cm/s,運動時間為t秒,0≤t≤5.
(1)AE=________,EF=__________
(2)若G,H分別是AB,DC中點,求證:四邊形EGFH是平行四邊形.(![]() 相遇時除外)
相遇時除外)
(3)在(2)條件下,當t為何值時,四邊形EGFH為矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
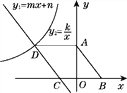
【題目】如圖,在菱形ABCD中,AD∥x軸,點A的坐標為(0,4),點B的坐標為(3,0).CD邊所在直線y1=mx+n與x軸交于點C,與雙曲線y2=![]() (x<0)交于點D.
(x<0)交于點D.
(1)求直線CD對應的函數表達式及k的值.
(2)把菱形ABCD沿y軸的正方向平移多少個單位后,點C落在雙曲線y2=![]() (x<0)上?
(x<0)上?
(3)直接寫出使y1>y2的自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=-![]() x2+
x2+![]() x-2與x軸相交于點A、B,與y軸相交于點C.
x-2與x軸相交于點A、B,與y軸相交于點C.
(1)求證:△AOC∽△COB;
(2)過點C作CD∥x軸交拋物線于點D.若點P在線段AB上以每秒1個單位的速度由A向B運動,同時點Q在線段CD上也以每秒1個單位的速度由D向C運動,則經過幾秒后,PQ=AC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,雙邊直尺有兩條平行的邊,但是沒有刻度,可以用來畫等距平行線:
![]()
我們也可用工具自制(如圖):
![]()
下面是小My同學設計的“過直線外一點作這條直線的平行線”的雙邊直尺作圖過程.
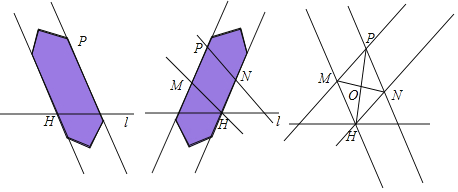
(1)根據小My同學的作圖過程,請證明O為PH中點.
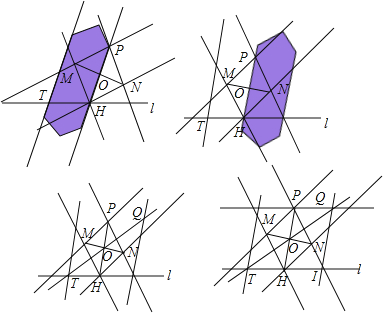
(2)根據小My同學的作圖過程,請證明PQ∥l.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O交BC于點D,過點D作DE⊥AC于點E.
(1)求證:DE是⊙O的切線.
(2)若∠B=30°,AB=8,求DE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 的頂點A、C分別在
的頂點A、C分別在![]() 、
、![]() 的正半軸上,反比例函數
的正半軸上,反比例函數![]() (
(![]() )與矩形
)與矩形![]() 的邊AB、BC交于點D、E.
的邊AB、BC交于點D、E.

(1)若![]() ,則
,則![]() 的面積為_________;
的面積為_________;
(2)若D為AB邊中點.
①求證:E為BC邊中點;
②若![]() 的面積為4,求
的面積為4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=5cm,∠ADC=120°,點E、F同時由A、C兩點出發,分別沿AB.CB方向向點B勻速移動(到點B為止),點E的速度為1cm/s,點F的速度為2cm/s,經過t秒△DEF為等邊三角形,則t的值為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com