
【題目】在△ABC中,∠C=α.⊙O是△ABC的內切圓,⊙P分別與CA的延長線、CB的延長線以及直線AB均只有一個公共點,⊙O的半徑為m,⊙P的半徑為n.

(1)當α=90°時,AC=6,BC=8時,m= ,n= .
(2)當α取下列度數時,求△ABC的面積(用含有m、n的代數式表示).
①如圖①,α=90°;
②如圖②,α=60°.
【答案】(1)2,12;(2)①mn;②![]() mn
mn
【解析】
(1)如圖①,設點D,E,F分別是3個切點,連接PD,PE,PF,連接OA,OB,OC,由勾股定理求得斜邊AB的長,再由面積法可得m的值,由正方形的性質及切線長定理可得n的值;
(2)①由于α=90°,與(1)中度數相同,故解題思路與(1)相同,僅需要將相關線段用m和n表示;
②連接CP,由切線長定理得∠PCE=30°,由含30°角的直角三角形的性質及面積法,可得答案.
(1)如圖①,設點D,E,F分別是3個切點,連接PD,PE,PF,連接OA,OB,OC.

∵AC=6,BC=8,∴AB=![]() =10.
=10.
∵S△BCA=S△ABO+S△ACO+S△BCO,∴![]() ×6×8=
×6×8=![]() ×10m+
×10m+![]() ×6m+
×6m+![]() ×8m,∴m=2.
×8m,∴m=2.
∵CD,CE是⊙P的切線,D、E為切點,∴CD=CE,∠PDC=∠PEC=90°.
∵∠ACB=90°,∴四邊形DPEC為正方形,∴n=PD=![]() .
.
由切線長定理可知,AF=AD,BF=BE,∴n=![]() =
=![]() =
=![]() =12;
=12;
(2)如圖①,由切線的性質,可知PD⊥CD,PE⊥BC,PF⊥AB,PD=PE=PF,設△ABC的面積為S△ABC,周長為C△ABC.
同(1),根據面積法可知m=![]() .
.
①如圖①.
∵n=![]() =
=![]() =
=![]() =
=![]() .
.
又∵m=![]() ,∴S△ABC=
,∴S△ABC=![]() =mn.
=mn.
②如圖②.
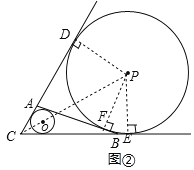
連接CP,由切線長定理得:
CD=CE=![]() =
=![]() =
=![]() =
=![]() .
.
∵PD⊥CD,PE⊥BC,∴CP平分∠ACB,∴∠PCE=30°,∴n=PE=![]() =
=![]() =
=![]() .
.
又∵m=![]() ,∴S△ABC=
,∴S△ABC=![]() =
=![]() mn.
mn.


科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,過點A(﹣![]() ,0)的兩條直線分別交y軸于B、C兩點,且B、C兩點的縱坐標分別是一元二次方程x2﹣2x﹣3=0的兩個根
,0)的兩條直線分別交y軸于B、C兩點,且B、C兩點的縱坐標分別是一元二次方程x2﹣2x﹣3=0的兩個根
(1)求線段BC的長度;
(2)試問:直線AC與直線AB是否垂直?請說明理由;
(3)若點D在直線AC上,且DB=DC,求點D的坐標;
(4)在(3)的條件下,直線BD上是否存在點P,使以A、B、P三點為頂點的三角形是等腰三角形?若存在,請直接寫出P點的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的頂點坐標分別為A(1,1),B(4,2),C(3,5).
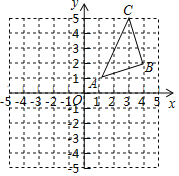
(1)求△ABC的面積;
(2)在圖中畫出△ABC繞點A逆時針旋轉90°得到的△A'B'C',并寫出點C的對應點C'的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,以
,以![]() 為直徑作⊙
為直徑作⊙![]() ,分別交
,分別交![]() ,
,![]() 于點
于點![]() ,
,![]() .
.
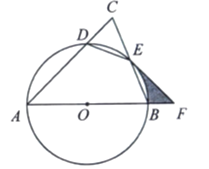
(1)求證:![]() ;
;
(2)若![]() ,求
,求![]() 的度數;
的度數;
(3)過點![]() 作⊙
作⊙![]() 的切線,交
的切線,交![]() 的延長線于點
的延長線于點![]() ,當
,當![]() 時,求圖中陰影部分的面積.
時,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
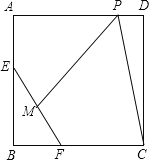
【題目】如圖,在邊長為8的正方形ABCD中,E、F分別是邊AB、BC上的動點,且EF=6,M為EF中點,P是邊AD上的一個動點,則CP+PM的最小值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋中有4個大小、質地完全相同的乒乓球,球面上分別標有數-1,2,-3,4.
(1)搖勻后任意摸出1個球,則摸出的乒乓球球面上的數是負數的概率為________.
(2)搖勻后先從中任意摸出1個球(不放回),再從余下的3個球中任意摸出1個球,用列表或畫樹狀圖的方法求兩次摸出的乒乓球球面上的數之和是正數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,一張矩形紙片ABCD,其中AD=8cm,AB=6cm,先沿對角線BD對折,點C落在點C′的位置,BC′交AD于點G.
(1)求證:AG=C′G;
(2)如圖2,再折疊一次,使點D與點A重合,得折痕EN,EN交AD于點M,求EM的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
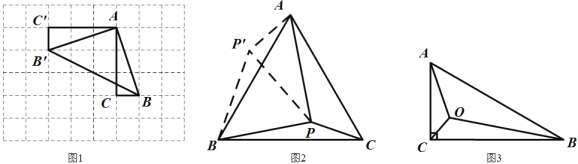
【題目】(1)如圖 1,在邊長為 1 個單位長度的小正方形組成的網格中,ABC 的三個頂點均在格點上.現將ABC 繞點 A 按順時針方向旋轉 90°,點 B 的對應點為B′,點 C 的對應點為C′, 連接 BB′,如圖所示則∠AB′B= .
(2)如圖 2,在等邊ABC 內有一點 P,且 PA=2,PB=![]() ,PC=1,如果將△BPC 繞點 B 逆時針旋轉 60°得出△ABP′,求∠BPC 的度數和 PP′的長;
,PC=1,如果將△BPC 繞點 B 逆時針旋轉 60°得出△ABP′,求∠BPC 的度數和 PP′的長;
(3)如圖3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點O為
,點O為![]() 內一點,連接AO,BO,CO,且
內一點,連接AO,BO,CO,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com