
【題目】某工藝品廠生產一種汽車裝飾品,每件生產成本為20元,銷售價格在30元至80元之間(含30元和80元),銷售過程中的管理、倉儲、運輸等各種費用(不含生產成本)總計50萬元,其銷售量y(萬個)與銷售價格(元/個)的函數關系如圖所示.
(1)當30≤x≤60時,求y與x的函數關系式;
(2)求出該廠生產銷售這種產品的純利潤w(萬元)與銷售價格x(元/個)的函數關系式;
(3)銷售價格應定為多少元時,獲得利潤最大,最大利潤是多少?

【答案】(1)y=﹣0.1x+8(30≤x≤60)(2)w= (3)當銷售價格定為50元/件或80元/件,獲得利潤最大,最大利潤是40萬元
(3)當銷售價格定為50元/件或80元/件,獲得利潤最大,最大利潤是40萬元
【解析】試題分析:(1)由圖象知,當30≤x≤60時,圖象過(60,2)和(30,5),運用待定系數法求解析式即可;
(2)根據銷售產品的純利潤=銷售量×單個利潤,分30≤x≤60和60<x≤80列函數表達式;
(3)當30≤x≤60時,運用二次函數性質解決,當60<x≤80時,運用反比例函數性質解答.
試題解析:(1)當x=60時,y=![]() =2,
=2,
∴當30≤x≤60時,圖象過(60,2)和(30,5),
設y=kx+b,則![]() ,
,
解得: ![]() ,
,
∴y=﹣0.1x+8(30≤x≤60);
(2)根據題意,當30≤x≤60時,W=(x﹣20)y﹣50=(x﹣20)(﹣0.1x+8)﹣50=![]() +10x﹣210,
+10x﹣210,
當60<x≤80時,W=(x﹣20)y﹣50=(x﹣20)![]() ﹣50=
﹣50=![]() +70,
+70,
綜上所述:W= ;
;
(3)當30≤x≤60時,W=![]() +10x﹣210=
+10x﹣210=![]() ,
,
當x=50時, ![]() =40(萬元);
=40(萬元);
當60<x≤80時,W=![]() +70,
+70,
∵﹣2400<0,W隨x的增大而增大,
∴當x=80時, ![]() =
=![]() +70=40(萬元),
+70=40(萬元),
答:當銷售價格定為50元/件或80元/件,獲得利潤最大,最大利潤是40萬元.


科目:初中數學 來源: 題型:
【題目】下列從左到右的變形中是因式分解的有( )
①x2﹣y2﹣1=(x+y)(x﹣y)﹣1;
②x3+x=x(x2+1);
③(x﹣y)2=x2﹣2xy+y2;
④x2﹣9y2=(x+3y)(x﹣3y).
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了選拔學生參加“漢字聽寫大賽”,對九年級一班、二班各10名學生進行漢字聽寫測試,計分采用10分制(得分均取整數),成績達到6分或6分以上為及格、達到9分或10分以上為優秀.這20位同學的成績與統計數據如下表:
序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均數 | 中位數 | 眾數 | 方差 | 及格率 | 優秀率 |
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表中,a= ,b= ;
(2)有人說二班的及格率、優秀率高于一班,所以二班的成績比一班好,但也有人堅持認為一班成績比二班好,請你給出支持一班成績好的兩條理由;
(3)若從這兩班獲滿分的同學中隨意抽1名同學參加“漢字聽寫大賽”,求參賽同學恰好是一班同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展“愛我海珠,創衛同行”的活動,倡議學生利用雙休日在海珠濕地公園參加義務勞動,為了解同學們勞動情況,學校隨機調查了部分同學的勞動時間,并用得到的數據繪制了不完整的統計圖,根據圖中信息解答下列問題:
(1)將條形統計圖補充完整.
(2)抽查的學生勞動時間的眾數為 , 中位數為 .
(3)已知全校學生人數為1200人,請你估算該校學生參加義務勞動1小時的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=8,BC=4,將△ADC沿AC折疊,點D落在點D′處,CD′與AB交于點F. 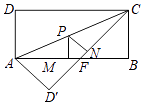
(1)求線段AF的長.
(2)求△AFC的面積.
(3)點P為線段AC(不含點A、C)上任意一點,PM⊥AB于點M,PN⊥CD′于點N,試求PM+PN的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com