
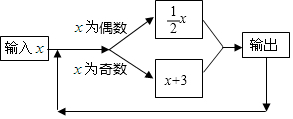
分析 (1)根據數值轉換機的運算程序,以及有理數的混合運算的運算方法,求出第1次輸入的數為2時,第2次輸出的數為多少,以及第1次輸入的數為12時,第5次輸出的數為多少即可.
(2)根據數值轉換機的運算程序,以及有理數的混合運算的運算方法,求出若輸入的數為5,每次輸出的數的規律,判斷出第2016次輸出的數是多少即可.
(3)根據數值轉換機的運算程序,求出所有x的值,使得輸入的數和第3次輸出的數相等即可.
解答 解:(1)∵1+3=4,
∴第1次輸出的數為1,則第2次輸出的數為4.
12×$\frac{1}{2}$=6,6×$\frac{1}{2}$=3,3+3=6,6×$\frac{1}{2}$=3,3+3=6,
∴第1次輸入的數為12,則第5次輸出的數為6.
(2)5+3=8,8×$\frac{1}{2}$=4,4×$\frac{1}{2}$=2,2×$\frac{1}{2}$=1,1+3=4,
∴若輸入的數為5,則每次輸出的數分別是8、4、2、1、4、2、1,…,
(2016-1)÷3
=2015÷3
=671…2
∴第2016次輸出的數是2.
(3)如圖,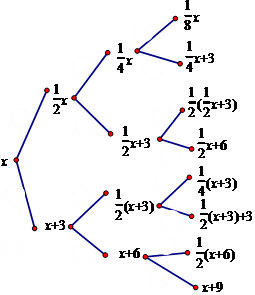 ,
,
由x=$\frac{1}{8}$x,解得x=0;符合題意;
由x=$\frac{1}{4}$x+3,解得x=4;符合題意,
由x=$\frac{1}{2}$($\frac{1}{2}$x+3),解得x=2;符合題意,
由x=$\frac{1}{2}$x+6,解得x=12;$\frac{1}{2}$x=6,偶數,不符合題意;
由x=$\frac{1}{4}$(x+3),解得x=1;符合題意;
由x=$\frac{1}{2}$(x+3)+3,解得x=9;x+3=12,是偶數,不符合題意,
由x=$\frac{1}{2}$(x+6),解得x=6;而x是偶數,不符合題意;
由x=x+9,解得x無解;
∴存在輸入的數x,使第3次輸出的數是x,此時x=0,1,2,4;
故答案為:4、6.
點評 此題主要考查了代數式求值問題,要熟練掌握,求代數式的值可以直接代入、計算.如果給出的代數式可以化簡,要先化簡再求值.題型簡單總結以下三種:①已知條件不化簡,所給代數式化簡;②已知條件化簡,所給代數式不化簡;③已知條件和所給代數式都要化簡.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
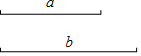 已知:線段a,b.
已知:線段a,b.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
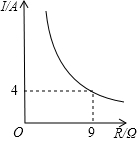 已知蓄電池的電壓U為定值,使用蓄電池時,電流I(單位:A)與電阻R(單位:Ω)是反比例函數關系,它的圖象如圖所示.
已知蓄電池的電壓U為定值,使用蓄電池時,電流I(單位:A)與電阻R(單位:Ω)是反比例函數關系,它的圖象如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com