【題目】如圖，函數
的圖象過點
．
求該函數的解析式；
過點
分別向
軸和
軸作垂線，垂足為
和
，求四邊形
的面積；
求證：過此函數圖象上任意一點分別向軸和軸作垂線，這兩條垂線與兩坐標軸所圍成矩形的面積為定值．
中考解讀考點精練系列答案科目：初中數學 來源： 題型：
【題目】A、B兩輛汽車同時從相距330千米的甲、乙兩地相向而行，s（千米）表示汽車與甲地的距離，t（分）表示汽車行駛的時間，如圖，L1，L2分別表示兩輛汽車的s與t的關系．
（1）L1表示哪輛汽車到甲地的距離與行駛時間的關系？
（2）汽車B的速度是多少？
（3）求L1，L2分別表示的兩輛汽車的s與t的關系式．
（4）2小時后，兩車相距多少千米？
（5）行駛多長時間后，A、B兩車相遇？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“綠水青山就是金山銀山”，為保護生態環境，A，B兩村準備各自清理所屬區域養魚網箱和捕魚網箱，每村參加清理人數及總開支如下表：
村莊 | 清理養魚網箱人數/人 | 清理捕魚網箱人數/人 | 總支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
（1）若兩村清理同類漁具的人均支出費用一樣，求清理養魚網箱和捕魚網箱的人均支出費用各是多少元；
（2）在人均支出費用不變的情況下，為節約開支，兩村準備抽調40人共同清理養魚網箱和捕魚網箱，要使總支出不超過102000元，且清理養魚網箱人數小于清理捕魚網箱人數，則有哪幾種分配清理人員方案？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料：
在學習《圓》這一章時，老師給同學們布置了一道尺規作圖題：
尺規作圖：過圓外一點作圓的切線．
已知：P為⊙O外一點．
求作：經過點P的⊙O的切線．
小敏的作法如下：如圖，
（1）連接OP，作線段OP的垂直平分線MN交OP于點C．
（2）以點C為圓心，CO的長為半徑作圓，交⊙O于A，B兩點．
（3）作直線PA，PB．
老師認為小敏的作法正確．
請回答：連接OA，OB后，可證∠OAP=∠OBP=90°，其依據是 ；由此可證明直線PA，PB都是⊙O的切線，其依據是 ．請寫出證明過程．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】等邊三角形ABC 中，BD是角平分線，點E在BC邊的延長線上，且CD=CE，則∠BDE的度數是（ ）
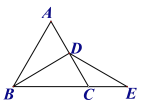
A.90°B.100°C.120°D.無法確定
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，AB＝2，點M為正方形ABCD的邊CD上的動點(與點C，D不重合)，連接BM，作MF⊥BM，與正方形ABCD的外角∠ADE的平分線交于點F.設CM＝x，△DFM的面積為y，則y與x之間的函數關系式為________________．
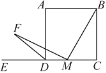
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】列方程解應用題：某商場經市場調查，預計一款夏季童裝能獲得市場青睞，便花費15000元購進了一批此款童裝，上市后很快售罄．該店決定繼續進貨，由于第二批進貨數量是第一批進貨數量的2倍，因此單價便宜了10元，購進第二批童裝一共花費了27000元．那該店所購進的第一批童裝的價格是多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線y=ax2+bx+c（a≠0）的對稱軸為直線x=1，與x軸的一個交點是點A（3，0），其部分圖象如圖，則下列結論：
①2a+b=0；
②b2﹣4ac＜0；
③一元二次方程ax2+bx+c=0（a≠0）的另一個解是x=﹣1；
④點（x1，y1），（x2，y2）在拋物線上，若x1＜0＜x2，則y1＜y2．
其中正確的結論是_____（把所有正確結論的序號都填在橫線上）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本題6分）如圖，已知△ABC，∠C=Rt∠，AC<BC，D為BC上一點，且到A，B兩點的距離相等．
（1）用直尺和圓規，作出點D的位置（不寫作法，保留作圖痕跡）；
（2）連結AD，若∠B=37°，求∠CAD的度數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
