
【題目】如圖是二次函數(shù)![]() 圖象的一部分,圖象過(guò)點(diǎn)
圖象的一部分,圖象過(guò)點(diǎn)![]() ,對(duì)稱(chēng)軸為直線
,對(duì)稱(chēng)軸為直線![]() ,給出四個(gè)結(jié)論:①
,給出四個(gè)結(jié)論:①![]() ; ②
; ②![]() ;③若點(diǎn)
;③若點(diǎn)![]() 、
、![]() 為函數(shù)圖象上的兩點(diǎn),則
為函數(shù)圖象上的兩點(diǎn),則![]() ;④關(guān)于
;④關(guān)于![]() 的方程
的方程![]() 一定有兩個(gè)不相等的實(shí)數(shù)根.其中,正確結(jié)論的是個(gè)數(shù)是( )
一定有兩個(gè)不相等的實(shí)數(shù)根.其中,正確結(jié)論的是個(gè)數(shù)是( )
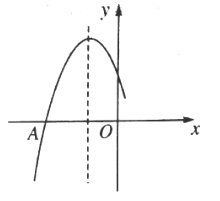
A.4B.3C.2D.1
【答案】C
【解析】
①根據(jù)拋物線開(kāi)口方向、對(duì)稱(chēng)軸及與y軸交點(diǎn)情況可判斷;②根據(jù)拋物線對(duì)稱(chēng)軸可判斷;③根據(jù)點(diǎn)離對(duì)稱(chēng)軸的遠(yuǎn)近可判斷;④根據(jù)拋物線與直線![]() 交點(diǎn)個(gè)數(shù)可判斷.
交點(diǎn)個(gè)數(shù)可判斷.
由圖象可知:開(kāi)口向下,故![]() ,
,
拋物線與y軸交點(diǎn)在x軸上方,故![]() >0,
>0,
∵對(duì)稱(chēng)軸![]() ,即
,即![]() 同號(hào),
同號(hào),
∴![]() ,
,
∴![]() ,故①正確;
,故①正確;
∵對(duì)稱(chēng)軸為![]() ,
,
∴![]() ,
,
∴![]() ,故②不正確;
,故②不正確;
∵拋物線是軸對(duì)稱(chēng)圖形,對(duì)稱(chēng)軸為![]() ,
,
點(diǎn)![]() 關(guān)于對(duì)稱(chēng)軸為
關(guān)于對(duì)稱(chēng)軸為![]() 的對(duì)稱(chēng)點(diǎn)為
的對(duì)稱(chēng)點(diǎn)為![]()
當(dāng)![]() 時(shí),
時(shí),
此時(shí)y隨![]() 的增大而減少,
的增大而減少,
∵3![]() 0,
0,
∴![]() ,故③錯(cuò)誤;
,故③錯(cuò)誤;
∵拋物線的頂點(diǎn)在第二象限,開(kāi)口向下,與![]() 軸有兩個(gè)交點(diǎn),
軸有兩個(gè)交點(diǎn),
∴拋物線![]() 與直線
與直線![]() 有兩個(gè)交點(diǎn),
有兩個(gè)交點(diǎn),
∴關(guān)于![]() 的方程
的方程![]() 有兩個(gè)不相等的實(shí)數(shù)根,所以④正確;
有兩個(gè)不相等的實(shí)數(shù)根,所以④正確;
綜上:①④正確,共2個(gè);
故選:C.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】小晗家客廳裝有一種三位單極開(kāi)關(guān),分別控制著A(樓梯)、B(客廳)、C(走廊)三盞電燈,在正常情況下,小晗按下任意一個(gè)開(kāi)關(guān)均可打開(kāi)對(duì)應(yīng)的一盞電燈,既可三盞、兩盞齊開(kāi),也可分別單盞開(kāi).因剛搬進(jìn)新房不久,不熟悉情況.
(1)若小晗任意按下一個(gè)開(kāi)關(guān),正好樓梯燈亮的概率是多少?
(2)若任意按下一個(gè)開(kāi)關(guān)后,再按下另兩個(gè)開(kāi)關(guān)中的一個(gè),則正好客廳燈和走廊燈同時(shí)亮的概率是多少?請(qǐng)用樹(shù)狀圖或列表法加以說(shuō)明.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩商場(chǎng)以同樣價(jià)格出售同樣的商品:并且又各自推出不同的優(yōu)惠方案,在甲商場(chǎng)累計(jì)購(gòu)物超過(guò)100元后,超出100元的部分按![]() 收費(fèi);在乙商場(chǎng)累計(jì)購(gòu)物超過(guò)50元后,超出50元的部分按
收費(fèi);在乙商場(chǎng)累計(jì)購(gòu)物超過(guò)50元后,超出50元的部分按![]() 收費(fèi).顧客到哪家商場(chǎng)購(gòu)物花費(fèi)少?
收費(fèi).顧客到哪家商場(chǎng)購(gòu)物花費(fèi)少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系中,一次函數(shù)![]() (a≠0)的圖象與反比例函數(shù)
(a≠0)的圖象與反比例函數(shù)![]() 的圖象交于第二、第四象限內(nèi)的A、B兩點(diǎn),與
的圖象交于第二、第四象限內(nèi)的A、B兩點(diǎn),與![]() 軸交于點(diǎn)C,過(guò)點(diǎn)A作AH⊥
軸交于點(diǎn)C,過(guò)點(diǎn)A作AH⊥![]() 軸,垂足為點(diǎn)H,OH=3,tan∠AOH=
軸,垂足為點(diǎn)H,OH=3,tan∠AOH=![]() ,點(diǎn)B的坐標(biāo)為(
,點(diǎn)B的坐標(biāo)為(![]() ,-2).
,-2).
(1)求該反比例函數(shù)和一次函數(shù)的解析式;
(2)求△AHO的周長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商店專(zhuān)門(mén)銷(xiāo)售某種品牌的玩具,成本為30元/件,每天的銷(xiāo)售量y(件)與銷(xiāo)售單價(jià)x(元)之間存在著如圖所示的一次函數(shù)關(guān)系.
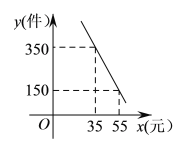
(1)求y與x之間的函數(shù)關(guān)系式;
(2)當(dāng)銷(xiāo)售單價(jià)為多少元時(shí),每天獲取的利潤(rùn)最大,最大利潤(rùn)是多少?
(3)為了保證每天的利潤(rùn)不低于3640元,試確定該玩具銷(xiāo)售單價(jià)的范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,以斜邊AB上一點(diǎn)O為圓心,OB為半徑作⊙O,交AC于點(diǎn)E,交AB于點(diǎn)D,且∠BEC=∠BDE.

(1)求證:AC是⊙O的切線;
(2)連接OC交BE于點(diǎn)F,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】直線l1:y=kx+b與直線l2:y=2x﹣4的交點(diǎn)M的縱坐標(biāo)為2,且與直線y=﹣x﹣2交x軸于同一點(diǎn).
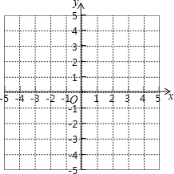
(1)求直線l1的表達(dá)式;
(2)在給出的平面直角坐標(biāo)系中作出直線l1的圖象,并求出它與直線l2及x軸圍成圖形的面積;
(3)根據(jù)圖象,直接寫(xiě)出關(guān)于x的不等式kx+b>0>2x﹣4的解集
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知△ABC內(nèi)接于⊙O,過(guò)點(diǎn)A作直線EF.
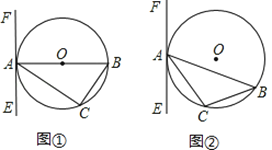
(1)如圖①所示,若AB為⊙O的直徑,要使EF成為⊙O的切線,還需要添加的一個(gè)條件是(至少說(shuō)出兩種): 或者 .
(2)如圖②所示,如果AB是不過(guò)圓心O的弦,且∠CAE=∠B,那么EF是⊙O的切線嗎?試證明你的判斷.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)![]() (m 為常數(shù)).
(m 為常數(shù)).
(1)證明:不論 m 為何值,該函數(shù)的圖像與 x 軸總有兩個(gè)公共點(diǎn);
(2)當(dāng) m 的值改變時(shí),該函數(shù)的圖像與 x 軸兩個(gè)公共點(diǎn)之間的距離是否改變?若不變, 請(qǐng)求出距離;若改變,請(qǐng)說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com