
【題目】綜合題
(1)【結論再現】如圖①,在 ![]() 中,
中, ![]() ,
, ![]() ,則
,則 ![]()
![]() ,
, ![]() .
. 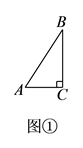
(2)【問題解決】
如圖②,四邊形 ![]() 是一張邊長為
是一張邊長為 ![]() 的正方形紙片,
的正方形紙片, ![]() 、
、 ![]() 分別為
分別為 ![]() 、
、 ![]() 的中點,沿過點
的中點,沿過點 ![]() 的折痕將紙片翻折,使點
的折痕將紙片翻折,使點 ![]() 落在
落在 ![]() 上的點
上的點 ![]() 處,折痕交
處,折痕交 ![]() 于點
于點 ![]() ,求
,求 ![]() 的度數和
的度數和 ![]() 的長.
的長.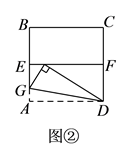
(3)【問題探究】
如圖③,點 ![]() 是等腰
是等腰 ![]() 斜邊
斜邊 ![]() 所在直線上一點,且滿足
所在直線上一點,且滿足 ![]() ,求
,求 ![]() 的大小和此時
的大小和此時 ![]() 的值.
的值.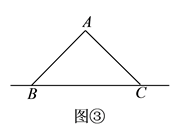
【答案】
(1)解: ![]() ,
,![]()
(2)解:∵ ![]() 折疊后得到
折疊后得到 ![]() ,
,
∴ ![]() ,且
,且 ![]() ,
,
∴在 ![]() 中,
中, ![]() ,sin∠FA′D=
,sin∠FA′D= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
在 ![]() 中,
中, ![]() ,
,
∴ ![]() ,
,
又∵在 ![]() 中,
中, ![]() ,那么
,那么 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
則 ![]() ,
,
那么 ![]()
![]()
![]()
(3)解:如圖,
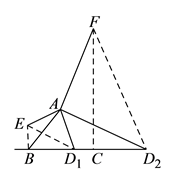
①當 ![]() 在
在 ![]() 邊上時,將線段
邊上時,將線段 ![]() 繞點
繞點 ![]() 順時針方向旋轉
順時針方向旋轉 ![]() 得到線段
得到線段 ![]() ,連接
,連接 ![]() ,
,
與(1)同理可證 ![]() ≌
≌ ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴四邊形 ![]() .
. ![]() 、
、 ![]() .
. ![]() 四點共圓,
四點共圓,
∴ ![]() ,
,
∴ ![]() .
.
②當 ![]() 在
在 ![]() 延長線上時,將線段
延長線上時,將線段 ![]() 繞點
繞點 ![]() 逆時針方向旋轉
逆時針方向旋轉 ![]() 得到線段
得到線段 ![]() ,連接
,連接 ![]() .
.
同理可證: ![]() ,
,
∵ ![]() ,∴四邊形
,∴四邊形 ![]() .
. ![]() .
. ![]() 、
、 ![]() 四點共圓,∴
四點共圓,∴ ![]() ,
,
∴ ![]() ,
,
綜上, ![]() 的度數為
的度數為 ![]() 或
或 ![]() .
.
比值計算如下:
過點 ![]() 作
作 ![]() ,如圖,
,如圖,
則在 ![]() 中,
中, ![]() ,
, ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
在 ![]() 中,
中, ![]() ,
,
設 ![]() ,
, ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)利用銳角三角函數的定義及特殊角的三角函數值,即可求出∠B的度數及![]() 的值。
的值。
(2)根據折疊的性質先求出∠FAD、∠EA′G的度數,再利用勾股定理在Rt△A′FD中求出A′F的長,即可得出A′E的長,再利用直角三角形的性質得出A′G的長,然后求出EG的長,從而得到BG的長。
(3)根據題意畫出圖形,分兩種情況討論:①當 D 在 B C 邊上時,將線段 A D 1 繞點 A 順時針方向旋轉 90 ° 得到線段 AE ,連接 BE ,先證明△ABE ≌ △ACD1 ,根據全等三角形的性質及特殊角的三角函數值求出 ∠BD1E=30°,得到四邊形 A . D1 、 B . E 四點共圓,然后根據圓周角定理即可求出結果;②當 D 在 B C 延長線上時,將線段 A D 繞點 A 逆時針方向旋轉 90 ° 得到線段 A F ,連接 C F .同①的方法類似求出結果即可,根據銳角三角函數的定義得出AD=![]() ,再求出ED的長,然后根據AD=
,再求出ED的長,然后根據AD=![]() x,即可求出結果。
x,即可求出結果。


科目:初中數學 來源: 題型:
【題目】為從甲、乙兩名射擊運動員中選出一人參加市錦標賽,特統計了他們最近10次射擊訓練的成績,其中,他們射擊的平均成績都為8.9環,方差分別是S甲2=0.8,S乙2=1.3,從穩定性的角度來看的成績更穩定.(填“甲”或“乙”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=-x+b的圖象與正比例函數y=kx的圖象都經過點B(3,1)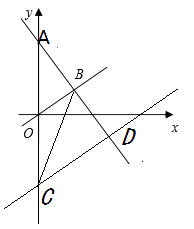
(1)求一次函數和正比例函數的表達式;
(2)若直線CD與正比例函數y=kx平行,且過點C(0,-4),與直線AB相交于點D,求點D的坐標.(注:二直線平行, ![]() 相等)
相等)
(3)連接CB,求三角形BCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小亮在同一條筆直的道路上進行 ![]() 米勻速跑步訓練,他們從同一地點出發,先到達終點的人原地休息,已知小明先出發
米勻速跑步訓練,他們從同一地點出發,先到達終點的人原地休息,已知小明先出發 ![]() 秒,在跑步的過程中,小明和小亮的距離
秒,在跑步的過程中,小明和小亮的距離 ![]() (米)與小亮出發的時間
(米)與小亮出發的時間 ![]() (秒)之間的函數關系如圖所示,則下列結論錯誤的是( ).
(秒)之間的函數關系如圖所示,則下列結論錯誤的是( ).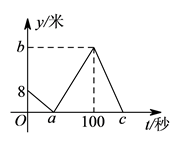
A.![]()
B.![]()
C.![]()
D.當 ![]() 時,
時, ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將拋物線y=x2﹣4x﹣3向左平移3個單位,再向上平移5個單位,得到拋物線的表達式為( )
A.y=(x+1)2﹣2
B.y=(x﹣5)2﹣2
C.y=(x﹣5)2﹣12
D.y=(x+1)2﹣12
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com