
【題目】定義:如果一個(gè)數(shù)的平方等于![]() ,記為
,記為![]() ,這個(gè)數(shù)
,這個(gè)數(shù)![]() 叫做虛數(shù)單位.那么和我們所學(xué)的實(shí)數(shù)對(duì)應(yīng)起來(lái)就叫做復(fù)數(shù),表示為
叫做虛數(shù)單位.那么和我們所學(xué)的實(shí)數(shù)對(duì)應(yīng)起來(lái)就叫做復(fù)數(shù),表示為![]() (
(![]() 為實(shí)數(shù)),
為實(shí)數(shù)),![]() 叫這個(gè)復(fù)數(shù)的實(shí)部,
叫這個(gè)復(fù)數(shù)的實(shí)部, ![]() 叫做這個(gè)復(fù)數(shù)的虛部,它的加,減,乘法運(yùn)算與整式的加,減,乘法運(yùn)算類(lèi)似.
叫做這個(gè)復(fù)數(shù)的虛部,它的加,減,乘法運(yùn)算與整式的加,減,乘法運(yùn)算類(lèi)似.
例如計(jì)算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ .
_________ .
(3)若兩個(gè)復(fù)數(shù)相等,則它們的實(shí)部和虛部必須分別相等,完成下列問(wèn)題:已知, ![]() ,(
,( ![]() 為實(shí)數(shù)),求
為實(shí)數(shù)),求![]() 的值.
的值.
(4)試一試:請(qǐng)利用以前學(xué)習(xí)的有關(guān)知識(shí)將![]() 化簡(jiǎn)成
化簡(jiǎn)成![]() 的形式.
的形式.
(5)解方程:x2 - 2x +4 = 0
【答案】(1) -I,1;(2)5,3+4i ;(3)x=-1,y=2;(4) i ;(5)x1= ![]() i ,x2=
i ,x2=![]() i
i
【解析】試題分析:(1)根據(jù)同底數(shù)冪的乘法法則、i2=﹣1計(jì)算即可;
(2)利用平方差公式、完全平方公式把原式展開(kāi),根據(jù)i2=﹣1計(jì)算即可;
(3)根據(jù)復(fù)數(shù)相等的條件解答即可;
(4)充分利用i2=﹣1計(jì)算,分子分母同時(shí)乘以(1+i)即可;
(5)計(jì)算出△=-3,根據(jù)虛數(shù)單位的定義即可求解.
試題解析:(1)i3=i2×i=-i,i4=(i2)2=(﹣1)2=1,故答案為:﹣i; 1;
(2)①(2+i)(2-i)=4-i2=4+1=5;
②(2+i)2=i2+4i+4=﹣1+4i+4=3+4i;
(3)根據(jù)復(fù)數(shù)相等的條件,得: ![]() ,解得:
,解得: ![]() ;
;
(4)![]() =
= =
=![]() =
=![]() =i;
=i;
(5)x2﹣2x+4=0,x=![]() =
=![]() =
=![]() ,
,
x1= ![]() ,x2=
,x2= ![]() .
.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系中,點(diǎn)O為坐標(biāo)原點(diǎn),拋物線y=ax2﹣2ax+![]() 與x軸交于點(diǎn)A、B(點(diǎn)A在點(diǎn)B的左側(cè)),拋物線的頂點(diǎn)為C,直線AC交y軸于點(diǎn)D,D為AC的中點(diǎn).
與x軸交于點(diǎn)A、B(點(diǎn)A在點(diǎn)B的左側(cè)),拋物線的頂點(diǎn)為C,直線AC交y軸于點(diǎn)D,D為AC的中點(diǎn).

(1)如圖1,求拋物線的頂點(diǎn)坐標(biāo);
(2)如圖2,點(diǎn)P為拋物線對(duì)稱(chēng)軸右側(cè)上的一動(dòng)點(diǎn),過(guò)點(diǎn)P作PQ⊥AC于點(diǎn)Q,設(shè)點(diǎn)P的橫坐標(biāo)為t,點(diǎn)Q的橫坐標(biāo)為m,求m與t的函數(shù)關(guān)系式;
(3)在(2)的條件下,如圖3,連接AP,過(guò)點(diǎn)C作CE⊥AP于點(diǎn)E,連接BE、CE分別交PQ于F、G兩點(diǎn),當(dāng)點(diǎn)F是PG中點(diǎn)時(shí),求點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】先化簡(jiǎn),再求值: ![]() ÷(
÷(![]() -a+2),其中a=2sin60°+3tan45°.
-a+2),其中a=2sin60°+3tan45°.
【答案】﹣![]() .
.
【解析】試題分析:先因式分解,再通分,約分化簡(jiǎn),代入數(shù)值求值.
試題解析:
解:原式= ![]() ÷(
÷(![]() -
-![]() )
)
=![]() ÷
÷![]() =
=![]() ,
,
∵a=2sin60°+3tan45°=2×![]() +3×1=
+3×1=![]() +3
+3
∴原式=![]() =﹣
=﹣![]() .
.
點(diǎn)睛:辨析分式與分式方程
分式,整式A除以整式B,可以表示成的![]() 的形式.如果B中含有字母,那么稱(chēng)
的形式.如果B中含有字母,那么稱(chēng) ![]() 為分式.分式特點(diǎn)是沒(méi)有等號(hào),分式加減一般需要通分.
為分式.分式特點(diǎn)是沒(méi)有等號(hào),分式加減一般需要通分.
(2)分式方程,分母中含有未知數(shù)的方程叫做分式方程.特點(diǎn)是有等號(hào),要先確定最簡(jiǎn)公分母,去分母的時(shí)候要每一項(xiàng)乘以最簡(jiǎn)公分母,所以一般不需要通分,而且要檢驗(yàn).
【題型】解答題
【結(jié)束】
22
【題目】圖1,圖2是兩張形狀和大小完全相同的方格紙,方格紙中每個(gè)小正方形的邊長(zhǎng)均為1,線段AB的兩個(gè)端點(diǎn)均在小正方形的頂點(diǎn)上.

(1)如圖1,在小正方形的頂點(diǎn)上確定一點(diǎn)C,連接AC、BC,使得△ABC為直角三角形,其面積為5,并直接寫(xiě)出△ABC的周長(zhǎng);
(2)如圖2,在小正方形的頂點(diǎn)上確定一點(diǎn)D,連接AD、BD,使得△ABD中有一個(gè)內(nèi)角為45°,且面積為3.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知四邊形ABCD是正方形,點(diǎn)B,C分別在直線![]() 和
和![]() 上,點(diǎn)A,D是x軸上兩點(diǎn).
上,點(diǎn)A,D是x軸上兩點(diǎn).

(1)若此正方形邊長(zhǎng)為2,k=_______.
(2)若此正方形邊長(zhǎng)為a,k的值是否會(huì)發(fā)生變化?若不會(huì)發(fā)生變化,請(qǐng)說(shuō)明理由;若會(huì)發(fā)生變化,求出a的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正方形網(wǎng)格圖中建立一直角坐標(biāo)系,一條圓弧經(jīng)過(guò)網(wǎng)格點(diǎn)A、B、C,請(qǐng)?jiān)诰W(wǎng)格中進(jìn)行下列操作:

(1)請(qǐng)?jiān)趫D中確定該圓弧所在圓心D點(diǎn)的位置,D點(diǎn)坐標(biāo)為 ;
(2)連接AD、CD,求⊙D的半徑及扇形DAC的圓心角度數(shù);
(3)若扇形DAC是某一個(gè)圓錐的側(cè)面展開(kāi)圖,求該圓錐的底面半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,觀察每個(gè)正多邊形中![]() 的變化情況,解答下列問(wèn)題:
的變化情況,解答下列問(wèn)題:
 ……
……
(1)將下面的表格補(bǔ)充完整:
正多邊形的邊數(shù) | 3 | 4 | 5 | 6 | …… |
|
| _________ | _________ | _________ | _________ | …… | _________ |
(2)根據(jù)規(guī)律,是否存在一個(gè)正![]() 邊形,使其中的
邊形,使其中的![]() ?若存在,寫(xiě)出
?若存在,寫(xiě)出![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
(3)根據(jù)規(guī)律,是否存在一個(gè)正![]() 邊形,使其中的
邊形,使其中的![]() ?若存在,寫(xiě)出
?若存在,寫(xiě)出![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,⊙O的半徑OD⊥弦AB于點(diǎn)C,連結(jié)AO并延長(zhǎng)交⊙O于點(diǎn)E,連結(jié)EC.若AB=8,CD=2,則EC的長(zhǎng)為( )

A. 2![]() B. 8 C. 2
B. 8 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為宣傳6月6日世界海洋日,某校八年級(jí)舉行了主題為“珍惜海洋資源,保護(hù)海洋生物多樣性”的知識(shí)競(jìng)賽活動(dòng).為了解全年級(jí)500名學(xué)生此次競(jìng)賽成績(jī)(百分制)的情況,隨機(jī)抽取了部分參賽學(xué)生的成績(jī),整理并繪制出如下不完整的統(tǒng)計(jì)表(表1)和統(tǒng)計(jì)圖(如圖).請(qǐng)根據(jù)圖表信息解答以下問(wèn)題:

(1)本次調(diào)查一共隨機(jī)抽取了個(gè)參賽學(xué)生的成績(jī);
(2)表1中a= ;
(3)所抽取的參賽學(xué)生的成績(jī)的中位數(shù)落在的“組別”是 ;
(4)請(qǐng)你估計(jì),該校九年級(jí)競(jìng)賽成績(jī)達(dá)到90分以上(含90分)的學(xué)生約有多少人.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB∥CD∥EF,CD交AF于G,
(1)如圖1,若CF平分∠AFE,∠A=70°,求∠C;
(2)如圖2,請(qǐng)寫(xiě)出∠A,∠C和∠AFC的數(shù)量關(guān)系并說(shuō)明理由.
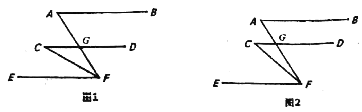
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com