
【題目】(問題背景)
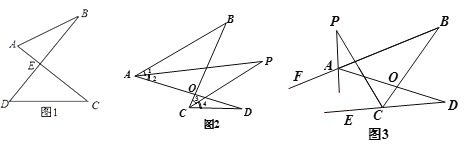
(1)如圖1的圖形我們把它稱為“8字形”,請說明∠A+∠B=∠C+∠D;
(簡單應用)
(2)如圖2, AP、CP分別平分∠BAD. ∠BCD,若∠ABC=46°,∠ADC=26°,求∠P的度數;
(問題探究)
(3)如圖3,直線AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,請猜想∠P的度數,并說明理由.
(拓展延伸)
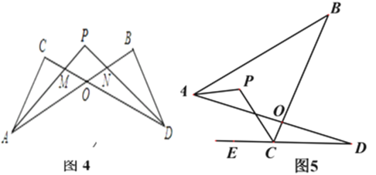
(4) ①在圖4中,若設∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,試問∠P與∠C、∠B之間的數量關系為: (用α、β表示∠P);
∠CDB,試問∠P與∠C、∠B之間的數量關系為: (用α、β表示∠P);
②在圖5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE, 猜想∠P與∠B、∠D的關系,直接寫出結論.
【答案】(1)見解析;(2)36°;(3)26°,理由見解析;(4)①∠P=![]() ②∠P=
②∠P=![]()
【解析】
(1)根據三角形內角和定理即可證明;
(2)直接利用(1)中的結論兩次,兩式相加,然后根據角平分線的性質求解即可;
(3)由AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,推出∠1=∠2,∠3=∠4,推出∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,由∠P+(180°﹣∠1)=∠D+(180°﹣∠3),∠P+∠1=∠B+∠4,推出2∠P=∠B+∠D,即可解決問題.
(4)①同法利用(1)種的結論列出方程即可解決問題.
②同法利用(1)種的結論列出方程即可解決問題.
(1)在△AEB中,∠A+∠B+∠AEB=180°.
在△CED中,∠C+∠D+∠CED=180°.
∵∠AEB=∠CED,
∴∠A+∠B=∠C+∠D;
(2)由(1)得:∠1+∠B=∠3+∠P,∠4+∠D=∠2+∠P,
∴∠1+∠B+∠4+∠D =∠3+∠P+∠2+∠P.
∵∠1=∠2,∠3=∠4,
∴2∠P=∠B+∠D=46°+26°=72°,
∴∠P=36°.
(3)∠P=26°,理由是:如圖3:
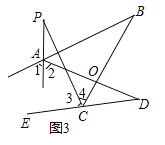
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°﹣∠2,∠PCD=180°﹣∠3.
∵∠PAB=∠1,∠P+∠PAB =∠B+∠4,
∴∠P+∠1=∠B+∠4.
∵∠P+(180°﹣∠2)=∠D+(180°﹣∠3),
∴2∠P=∠B+∠D,
∴∠P=![]() (∠B+∠D)=
(∠B+∠D)=![]() ×(36°+16°)=26°.
×(36°+16°)=26°.
(4)①設∠CAP=m,∠CDP=n,則∠CAB=3m,,∠CDB=3n,
∴∠PAB=2m,∠PDB=2n.
∵∠C+∠CAP=∠P+∠PDC,∠P+∠PAB=∠B+∠PDB,
∵∠C=α,∠B=β,
∴α+m=∠P+n,∠P+2m=β+2n,
∴α-∠P = n-m,∠P-β=2n-2m=2(n-m),
∴2α+β=3∠P
∴∠P=![]() .
.
故答案為:∠P=![]() .
.
②設∠BAP=x,∠PCE=y,則∠PAO=x,∠PCB=y.
∵∠PAO+∠P=∠PCD+∠D,∠B+∠BAO=∠OCD+∠D,
∴x+∠P=180°-y+∠D,∠B+2x=180°-2y+∠D,
∴∠P=![]() .
.
故答案為:∠P=![]() .
.


科目:初中數學 來源: 題型:
【題目】已知二次函數y=a(x﹣h)2+k(a,h,k為常數)在坐標平面上的圖象通過(0,5)、(15,8)兩點.若a<0,0<h<10,則h之值可能為下列何值?( )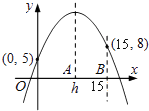
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小剛從點 ![]() 出發,沿著坡度為
出發,沿著坡度為 ![]() 的斜坡向上走了650米到達點
的斜坡向上走了650米到達點 ![]() ,且
,且 ![]() .
.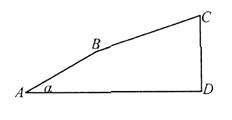
(1)則他上升的高度是 米 ;
(2)然后又沿著坡度為 ![]() 的斜坡向上走了1000米達到點
的斜坡向上走了1000米達到點 ![]() .問小剛從
.問小剛從 ![]() 點到
點到 ![]() 點上升的高度
點上升的高度 ![]() 是多少米(結果保留根號)?
是多少米(結果保留根號)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系 ![]() 中,矩形
中,矩形 ![]() 的邊
的邊 ![]() 在
在 ![]() 軸上,頂點
軸上,頂點 ![]() 在拋物線
在拋物線 ![]() 上,且拋物線交
上,且拋物線交 ![]() 軸于另一點
軸于另一點 ![]() .
.
(1)則 ![]() = ,
= , ![]() =;
=;
(2)已知 ![]() 為
為 ![]() 邊上一個動點(不與
邊上一個動點(不與 ![]() 、
、 ![]() 重合),連結
重合),連結 ![]() 交
交 ![]() 于點
于點 ![]() ,過點
,過點 ![]() 作
作 ![]() 軸的平行線分別交拋物線、直線
軸的平行線分別交拋物線、直線 ![]() 于
于 ![]() 、
、 ![]() .
.
①求線段 ![]() 的最大值,此時
的最大值,此時 ![]() 的面積為;
的面積為;
②若以點 ![]() 為圓心,
為圓心, ![]() 為半徑作⊙O,試判斷直線
為半徑作⊙O,試判斷直線 ![]() 與⊙O的能否相切,若能請求出
與⊙O的能否相切,若能請求出 ![]() 點坐標,若不能請說明理由.
點坐標,若不能請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
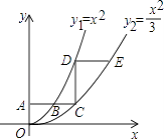
【題目】如圖,平行于x軸的直線AC分別交函數y1=x2(x≥0)與y2= ![]() (x≥0)的圖象于B、C兩點,過點C作y軸的平行線交y1的圖象于點D,直線DE∥AC,交y2的圖象于點E,則
(x≥0)的圖象于B、C兩點,過點C作y軸的平行線交y1的圖象于點D,直線DE∥AC,交y2的圖象于點E,則 ![]() = .
= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,EF∥AD,∠1=∠2.證明:∠DGA+∠BAC=180°.請完成說明過程.
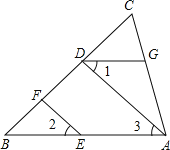
解:∵EF∥AD,(已知)
∴∠2=∠3.( )
又∵∠1=∠2(已知)
∴∠1=∠3,(等量代換)
∴AB∥ ,( )
∴∠DGA+∠BAC=180°.( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAC 的角平分線與 BC 的垂直平分線交于點 D,DE⊥AB, DF⊥AC,垂足分別為 E,F.若 AB=10,AC=8,求 BE 長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學家華羅庚在一次出國訪問途中,看到飛機上鄰座的乘客閱讀的雜志上有一道智力題:求59319的立方根.華羅庚脫口而出:39.眾人感覺十分驚奇,請華羅庚給大家解讀其中的奧秘.
你知道怎樣迅速準確的計算出結果嗎?請你按下面的問題試一試:
①![]() ,又
,又![]() ,
,
![]() ,∴能確定59319的立方根是個兩位數.
,∴能確定59319的立方根是個兩位數.
②∵59319的個位數是9,又![]() ,∴能確定59319的立方根的個位數是9.
,∴能確定59319的立方根的個位數是9.
③如果劃去59319后面的三位319得到數59,
而![]() ,則
,則![]() ,可得
,可得![]() ,
,
由此能確定59319的立方根的十位數是3
因此59319的立方根是39.
(1)現在換一個數195112,按這種方法求立方根,請完成下列填空.
①它的立方根是_______位數.
②它的立方根的個位數是_______.
③它的立方根的十位數是__________.
④195112的立方根是________.
(2)請直接填寫結果:
①![]() ________.
________.
②![]() ________.
________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列條件中,不能判斷△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com