
【題目】某批發城在冬天到來之際進了一批保暖衣,男生的保暖衣每件價格60元,女生的保暖衣每件價格40元,第一批共購買100件.
(1)第一批購買的保暖衣的總費用不超過5400元,求女生保暖衣最少購買多少件?
(2)第二批購買保暖衣,購買男、女生保暖衣的件數比為![]() ,價格保持第一批的價格不變;第三批購買男生保暖衣的價格在第一批購買的價格上每件減少了
,價格保持第一批的價格不變;第三批購買男生保暖衣的價格在第一批購買的價格上每件減少了![]() 元 ,女生保暖衣的價格比第一批購買的價格上每件增加了
元 ,女生保暖衣的價格比第一批購買的價格上每件增加了![]() 元,男生保暖衣的數量比第二批增加了
元,男生保暖衣的數量比第二批增加了![]() ,女生保暖衣的數量比第二批減少了
,女生保暖衣的數量比第二批減少了![]() ,第二批與第三批購買保暖衣的總費用相同,求
,第二批與第三批購買保暖衣的總費用相同,求![]() 的值.
的值.
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過點
經過點![]() ,
,![]() .
.

(1)求點B的坐標和拋物線的解析式;
(2)M(m,0)為x軸上一個動點,過點M垂直于x軸的直線與直線AB和拋物線分別交于點P、N,
①點![]() 在線段
在線段![]() 上運動,若以
上運動,若以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,求點
相似,求點![]() 的坐標;
的坐標;
②點![]() 在
在![]() 軸上自由運動,若三個點
軸上自由運動,若三個點![]() ,
,![]() ,
,![]() 中恰有一點是其它兩點所連線段的中點(三點重合除外),則稱
中恰有一點是其它兩點所連線段的中點(三點重合除外),則稱![]() ,
,![]() ,
,![]() 三點為“共諧點”.請直接寫出使得
三點為“共諧點”.請直接寫出使得![]() ,
,![]() ,
,![]() 三點成為“共諧點”的
三點成為“共諧點”的![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC中,AB=AC,∠ABC=α,過點A作直線MN,使MN∥BC,點D在直線MN上,作射線BD,將射線BD繞點B順時針旋轉角α后交直線AC于點E.
(1)如圖①,當α=60°,且點D在射線AN上時,直接寫出線段AB,AD,AE的數量關系.
(2)如圖②,當α=45°,且點D在射線AN上時,直寫出線段AB、AD、AE的數量關系,并說明理由.
(3)當α=30°時,若點D在射線AM上,∠ABE=15°,AD=![]() ﹣1,請直接寫出線段AE的長度.
﹣1,請直接寫出線段AE的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
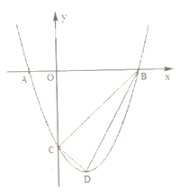
【題目】如圖,拋物線![]() 與軸交于
與軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,設拋物線的頂點為點
,設拋物線的頂點為點![]() .
.
(1)求該拋物線的解析式與頂點![]() 的坐標.
的坐標.
(2)試判斷![]() 的形狀,并說明理由.
的形狀,并說明理由.
(3)坐標軸上是否存在點![]() ,使得以
,使得以![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請直接寫出點
相似?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
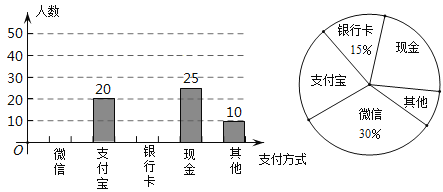
【題目】中國的數字支付正在引領未來世界的支付方式變革,中國消費者的移動支付比美國的移動支付要多出11倍,所以當我們展望數字錢包的未來時,中國是一個自然的起點.某校數學興趣小組設計了一份調查問卷,要求每人選且只選一種你最喜歡的支付方式.現將調查結果進行統計并繪制成如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:
(1)這次活動共調查了 人;在扇形統計圖中,表示“支付寶”支付的扇形圓心角的度數為 ;
(2)將條形統計圖補充完整.觀察此圖,將各種支付方式調查人數組成一組數據,求這組數據的“中位數”是“ ”;
(3)在一次購物中,小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付,請用畫樹狀圖或列表格的方法,求兩人選同種支付方式的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某店在開學初用880元購進若干個學生專用科學計算器,按每個50元出售,很快就銷售一空,據了解學生還急需3倍這種計算器,于是又用2580元購進所需計算器,由于量大每個進價比上次優惠1元,該店仍按每個50元銷售,最后剩下4個按九折賣出.這筆生意該店共盈利( )元.
A.508 B.520 C.528 D.560
查看答案和解析>>
科目:初中數學 來源: 題型:
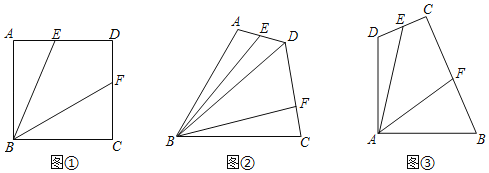
【題目】提出問題:(1)如圖①,正方形ABCD中,點E,點F分別在邊AD和邊CD上,若正方形邊長為4,DE+DF=4,則四邊形BEDF的面積為 .
探究問題:(2)如圖②,四邊形ABCD,AB=BC=4,∠ABC=60°,∠ADC=120°,點E、F分別是邊AD和邊DC上的點,連接BE,BF,若ED+DF=3,BD=2![]() ,求四邊形EBFD的面積;
,求四邊形EBFD的面積;
解決問題:(3)某地質勘探隊為了進行資源助測,建立了如圖③所示的一個四邊形野外勘查基地,基地相鄰兩側邊界DA、AB長度均為4km,∠DAB=90°,由于勘測需要及技術原因,主勘測儀C與基地邊緣D、B夾角為90°(∠DCB=90°),在邊界CD和邊界BC上分別有兩個輔助勘測儀E和F,輔助勘測儀E和F與主勘測儀C的距離之和始終等于4km(CE+CF=4).為了達到更好監測效果,需保證勘測區域(四邊形EAFC)面積盡可能大.請問勘測區域面積有沒有最大值,如果有求出最大值,如果沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】盒中有若干枚黑棋和白棋,這些棋除顏色外無其他差別,現讓學生進行摸棋試驗:每次摸出一枚棋,記錄顏色后放回搖勻.重復進行這樣的試驗得到以下數據:
摸棋的次數n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次數m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的頻率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根據表中數據估計從盒中摸出一枚棋是黑棋的概率是 ;(精確到0.01)
(2)若盒中黑棋與白棋共有4枚,某同學一次摸出兩枚棋,請計算這兩枚棋顏色不同的概率,并說明理由
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com