
【題目】如圖,已知△ABC,AB=BC,以AB為直徑的圓交AC于點D,過點D的⊙O的切線交BC于點E.若CD=5,CE=4,則⊙O的半徑是( ) 
A.3
B.4
C.![]()
D.![]()
【答案】D
【解析】解:如圖1,連接OD、BD, 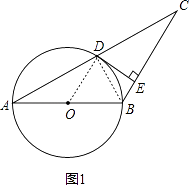 ,
,
∵AB是⊙O的直徑,
∴∠ADB=90°,
∴BD⊥AC,
又∵AB=BC,
∴AD=CD,
又∵AO=OB,
∴OD是△ABC的中位線,
∴OD∥BC,
∵DE是⊙O的切線,
∴DE⊥OD,
∴DE⊥BC,
∵CD=5,CE=4,
∴DE= ![]() ,
,
∵S△BCD=BDCD÷2=BCDE÷2,
∴5BD=3BC,
∴ ![]() ,
,
∵BD2+CD2=BC2 ,
∴ ![]() ,
,
解得BC= ![]() ,
,
∵AB=BC,
∴AB= ![]() ,
,
∴⊙O的半徑是;![]() .
.
故選:D.
首先連接OD、BD,判斷出OD∥BC,再根據DE是⊙O的切線,推得DE⊥OD,所以DE⊥BC;然后根據DE⊥BC,CD=5,CE=4,求出DE的長度是多少;最后判斷出BD、AC的關系,根據勾股定理,求出BC的值是多少,再根據AB=BC,求出AB的值是多少,即可求出⊙O的半徑是多少.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:初中數學 來源: 題型:
【題目】已知△ABC是等邊三角形.
(1)動手操作:如圖1,點D在△ABC內,且∠BDC=150°,CD=1,BD=![]() , 把△BCD繞著點C順時針旋轉,使點B旋轉到點A,得到△AEC.
, 把△BCD繞著點C順時針旋轉,使點B旋轉到點A,得到△AEC.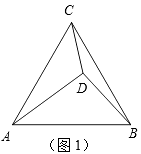
①依題意補全圖1;(確認無誤后,請用黑色水筆描黑)
②連接DE,則線段DE= , AD=;
(2)應用拓展:如圖2,點D在△ABC外,且CD=3,BD=4,AD=5,求∠BDC的度數.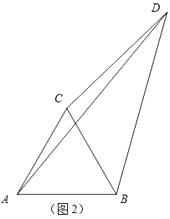
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一列快車從甲地勻速駛往乙地,一列慢車從乙地勻速駛往甲地,兩車同時出發,快車到達乙地后,快車停止運動,慢車繼續以原速勻速駛往甲地,直至慢車到達甲地為止,設慢車行駛的時間為t(h),兩車之間的距離為s(km),圖中的折線表示s與t之間的函數關系.根據圖象提供的信息有下列說法:①甲、乙兩地之間的距離為900km;②行駛4h兩車相遇;③快車的速度為150km/h;④行駛6h兩車相距400km;⑤相遇時慢車行駛了240km;⑥快車共行駛了6h.其中符合圖象描述的說法有( )個. 
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=kx+b的圖象與反比例函數y2= ![]() 的圖象相交于A,B兩點,直線AB與x軸相交于點C,點B的坐標為(﹣6,m),線段OA=5,E為x軸正半軸上一點,且cos∠AOE=
的圖象相交于A,B兩點,直線AB與x軸相交于點C,點B的坐標為(﹣6,m),線段OA=5,E為x軸正半軸上一點,且cos∠AOE= ![]() .
. 
(1)求反比例函數的解析式;
(2)求證:S△AOC=2S△BOC;
(3)直接寫出當y1>y2時,x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1中的摩天輪可抽象成一個圓,圓上一點離地面的高度y(m)與旋轉時間x(min)之間的關系如圖2所示. 
(1)根據圖2填表:
x(min) | 0 | 3 | 6 | 8 | 12 | … |
y(m) | … |
(2)變量y是x的函數嗎?為什么?
(3)根據圖中的信息,請寫出摩天輪的直徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明在課外學習時遇到這樣一個問題:
定義:如果二次函數y=a1x2+b1x+c1(a1≠0,a1 , b1 , c1是常數)與y=a2x2+b2x+c2(a2≠0,a2 , b2 , c2是常數)滿足a1+a2=0,b1=b2 , c1+c2=0,則稱這兩個函數互為“旋轉函數”.
求函數y=﹣x2+3x﹣2的“旋轉函數”.
小明是這樣思考的:由函數y=﹣x2+3x﹣2可知,a1=﹣1,b1=3,c1=﹣2,根據a1+a2=0,b1=b2 , c1+c2=0,求出a2 , b2 , c2 , 就能確定這個函數的“旋轉函數”.
請參考小明的方法解決下面問題:
(1)寫出函數y=﹣x2+3x﹣2的“旋轉函數”;
(2)若函數y=﹣x2+ ![]() mx﹣2與y=x2﹣2nx+n互為“旋轉函數”,求(m+n)2015的值;
mx﹣2與y=x2﹣2nx+n互為“旋轉函數”,求(m+n)2015的值;
(3)已知函數y=﹣ ![]() (x+1)(x﹣4)的圖象與x軸交于點A、B兩點,與y軸交于點C,點A、B、C關于原點的對稱點分別是A1 , B1 , C1 , 試證明經過點A1 , B1 , C1的二次函數與函數y=﹣
(x+1)(x﹣4)的圖象與x軸交于點A、B兩點,與y軸交于點C,點A、B、C關于原點的對稱點分別是A1 , B1 , C1 , 試證明經過點A1 , B1 , C1的二次函數與函數y=﹣ ![]() (x+1)(x﹣4)互為“旋轉函數.”
(x+1)(x﹣4)互為“旋轉函數.”
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣ ![]() x2+mx+n與x軸交于A (﹣2,0)、B兩點,與y軸交于點C.拋物線對稱軸為直線x=3,且對稱軸與x軸交于點D.
x2+mx+n與x軸交于A (﹣2,0)、B兩點,與y軸交于點C.拋物線對稱軸為直線x=3,且對稱軸與x軸交于點D.
(1)求拋物線的解析式;
(2)點P在線段BC上從點C開始向點B運動(點P不與點B、C重合),速度為每秒 ![]() 個單位,設運動時間為t(單位:s),過點P作x軸的垂線與拋物線相交于點F.求四邊形CDBF的面積S關于t的函數關系式.
個單位,設運動時間為t(單位:s),過點P作x軸的垂線與拋物線相交于點F.求四邊形CDBF的面積S關于t的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、B是圓O上的兩點,∠AOB=120°,C是AB弧的中點.
(1)求證:AB平分∠OAC;
(2)延長OA至P使得OA=AP,連接PC,若圓O的半徑R=1,求PC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形ABOC的頂點O在坐標原點,邊BO在x軸的負半軸上,頂點C的坐標為(﹣ ![]() ,3),反比例函數y=
,3),反比例函數y= ![]() 的圖象與菱形對角線AO交于D點,連接BD,當BD⊥x軸時,k的值是( )
的圖象與菱形對角線AO交于D點,連接BD,當BD⊥x軸時,k的值是( ) 
A.4 ![]()
B.﹣4 ![]()
C.2 ![]()
D.﹣2 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com