
【題目】如圖,在平面直角坐標(biāo)系中,拋物線(xiàn)y=﹣![]() x2+bx+c與x軸交于B,C兩點(diǎn),與y軸交于點(diǎn)A,直線(xiàn)y=﹣
x2+bx+c與x軸交于B,C兩點(diǎn),與y軸交于點(diǎn)A,直線(xiàn)y=﹣![]() x+2經(jīng)過(guò)A,C兩點(diǎn),拋物線(xiàn)的對(duì)稱(chēng)軸與x軸交于點(diǎn)D,直線(xiàn)MN與對(duì)稱(chēng)軸交于點(diǎn)G,與拋物線(xiàn)交于M,N兩點(diǎn)(點(diǎn)N在對(duì)稱(chēng)軸右側(cè)),且MN∥x軸,MN=7.
x+2經(jīng)過(guò)A,C兩點(diǎn),拋物線(xiàn)的對(duì)稱(chēng)軸與x軸交于點(diǎn)D,直線(xiàn)MN與對(duì)稱(chēng)軸交于點(diǎn)G,與拋物線(xiàn)交于M,N兩點(diǎn)(點(diǎn)N在對(duì)稱(chēng)軸右側(cè)),且MN∥x軸,MN=7.
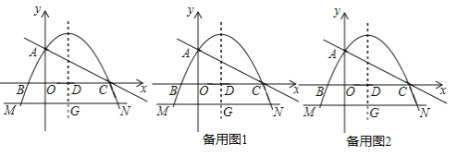
(1)求此拋物線(xiàn)的解析式.
(2)求點(diǎn)N的坐標(biāo).
(3)過(guò)點(diǎn)A的直線(xiàn)與拋物線(xiàn)交于點(diǎn)F,當(dāng)tan∠FAC=![]() 時(shí),求點(diǎn)F的坐標(biāo).
時(shí),求點(diǎn)F的坐標(biāo).
(4)過(guò)點(diǎn)D作直線(xiàn)AC的垂線(xiàn),交AC于點(diǎn)H,交y軸于點(diǎn)K,連接CN,△AHK沿射線(xiàn)AC以每秒1個(gè)單位長(zhǎng)度的速度移動(dòng),移動(dòng)過(guò)程中△AHK與四邊形DGNC產(chǎn)生重疊,設(shè)重疊面積為S,移動(dòng)時(shí)間為t(0≤t≤![]() ),請(qǐng)直接寫(xiě)出S與t的函數(shù)關(guān)系式.
),請(qǐng)直接寫(xiě)出S與t的函數(shù)關(guān)系式.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)點(diǎn)N的坐標(biāo)為(5,-3);(3)點(diǎn)F的坐標(biāo)為:(3,2)或(
x+2;(2)點(diǎn)N的坐標(biāo)為(5,-3);(3)點(diǎn)F的坐標(biāo)為:(3,2)或(![]() ,﹣
,﹣![]() );(4)
);(4)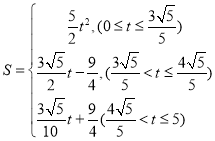 .
.
【解析】
(1)點(diǎn)A、C的坐標(biāo)分別為(0,2)、(4,0),將點(diǎn)A、C坐標(biāo)代入拋物線(xiàn)表達(dá)式即可求解;
(2)拋物線(xiàn)的對(duì)稱(chēng)軸為:x=![]() ,點(diǎn)N的橫坐標(biāo)為:
,點(diǎn)N的橫坐標(biāo)為:![]() ,即可求解;
,即可求解;
(3)分點(diǎn)F在直線(xiàn)AC下方、點(diǎn)F在直線(xiàn)AC的上方兩種情況,分別求解即可;
(4)分0≤t≤![]() 、當(dāng)
、當(dāng)![]() <t≤
<t≤![]() 、
、![]() <t≤
<t≤![]() 三種情況,分別求解即可.
三種情況,分別求解即可.
解:(1)直線(xiàn)y=﹣![]() x+2經(jīng)過(guò)A,C兩點(diǎn),則點(diǎn)A、C的坐標(biāo)分別為(0,2)、(4,0),
x+2經(jīng)過(guò)A,C兩點(diǎn),則點(diǎn)A、C的坐標(biāo)分別為(0,2)、(4,0),
則c=2,拋物線(xiàn)表達(dá)式為:y=﹣![]() x2+bx+2,
x2+bx+2,
將點(diǎn)C坐標(biāo)代入上式并解得:b=![]() ,
,
故拋物線(xiàn)的表達(dá)式為:y=﹣![]() x2+
x2+![]() x+2…①;
x+2…①;
(2)拋物線(xiàn)的對(duì)稱(chēng)軸為:x=![]() ,
,
點(diǎn)N的橫坐標(biāo)為: ![]() ,
,
故點(diǎn)N的坐標(biāo)為(5,-3);
(3)∵tan∠ACO=![]() =tan∠FAC=
=tan∠FAC=![]() ,
,
即∠ACO=∠FAC,
①當(dāng)點(diǎn)F在直線(xiàn)AC下方時(shí),
設(shè)直線(xiàn)AF交x軸于點(diǎn)R,
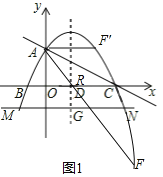
∵∠ACO=∠FAC,則AR=CR,
設(shè)點(diǎn)R(r,0),則r2+4=(r﹣4)2,解得:r=![]() ,
,
即點(diǎn)R的坐標(biāo)為:(![]() ,0),
,0),
將點(diǎn)R、A的坐標(biāo)代入一次函數(shù)表達(dá)式:y=mx+n得: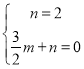 ,
,
解得: ,
,
故直線(xiàn)AR的表達(dá)式為:y=﹣![]() x+2…②,
x+2…②,
聯(lián)立①②并解得:x=![]() ,故點(diǎn)F(
,故點(diǎn)F(![]() ,﹣
,﹣![]() );
);
②當(dāng)點(diǎn)F在直線(xiàn)AC的上方時(shí),
∵∠ACO=∠F′AC,∴AF′∥x軸,
則點(diǎn)F′(3,2);
綜上,點(diǎn)F的坐標(biāo)為:(3,2)或(![]() ,﹣
,﹣![]() );
);
(4)如圖2,設(shè)∠ACO=α,則tanα=![]() ,則sinα=
,則sinα=![]() ,cosα=
,cosα=![]() ;
;
①當(dāng)0≤t≤![]() 時(shí)(左側(cè)圖),
時(shí)(左側(cè)圖),
設(shè)△AHK移動(dòng)到△A′H′K′的位置時(shí),直線(xiàn)H′K′分別交x軸于點(diǎn)T、交拋物線(xiàn)對(duì)稱(chēng)軸于點(diǎn)S,
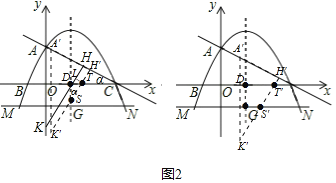
則∠DST=∠ACO=α,過(guò)點(diǎn)T作TL⊥KH,
則LT=HH′=t,∠LTD=∠ACO=α,
則DT= ,DS=
,DS=![]() ,
,
S=S△DST=![]() DT×DS=
DT×DS=![]() ;
;
②當(dāng)![]() <t≤
<t≤![]() 時(shí)(右側(cè)圖),
時(shí)(右側(cè)圖),
同理可得:
S=![]() =
=![]() DG×(GS′+DT′)=
DG×(GS′+DT′)=![]() 3+(
3+(![]() +
+![]() ﹣
﹣![]() )=
)=![]() ;
;
③當(dāng)![]() <t≤
<t≤![]() 時(shí),同理可得S=
時(shí),同理可得S=![]() ;
;
綜上,S= .
.


 期末1卷素質(zhì)教育評(píng)估卷系列答案
期末1卷素質(zhì)教育評(píng)估卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】△ABC中,∠C=90°,∠A=60°,AC=2cm.長(zhǎng)為1cm的線(xiàn)段MN在△ABC的邊AB上沿AB方向以1cm/s的速度向點(diǎn)B運(yùn)動(dòng)(運(yùn)動(dòng)前點(diǎn)M與點(diǎn)A重合).過(guò)M,N分別作AB的垂線(xiàn)交直角邊于P,Q兩點(diǎn),線(xiàn)段MN運(yùn)動(dòng)的時(shí)間為ts.
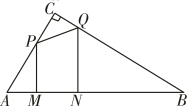
(1)當(dāng)(0≤t≤1)時(shí),PM=____________ ,QN=___________(用t的代數(shù)式表示);
(2)線(xiàn)段MN運(yùn)動(dòng)過(guò)程中,四邊形MNQP有可能成為矩形嗎?若有可能,求出此時(shí)t的值;若不可能,說(shuō)明理由;
(3)t為何值時(shí),以C,P,Q為頂點(diǎn)的三角形與△ABC相似?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知直線(xiàn)l:y=﹣x+4分別與x軸、y軸交于點(diǎn)A,B,雙曲線(xiàn)![]() (k>0,x>0)與直線(xiàn)l不相交,E為雙曲線(xiàn)上一動(dòng)點(diǎn),過(guò)點(diǎn)E作EG⊥x軸于點(diǎn)G,EF⊥y軸于點(diǎn)F,分別與直線(xiàn)l交于點(diǎn)C,D,且∠COD=45°,則k=_____.
(k>0,x>0)與直線(xiàn)l不相交,E為雙曲線(xiàn)上一動(dòng)點(diǎn),過(guò)點(diǎn)E作EG⊥x軸于點(diǎn)G,EF⊥y軸于點(diǎn)F,分別與直線(xiàn)l交于點(diǎn)C,D,且∠COD=45°,則k=_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某數(shù)學(xué)興趣小組為測(cè)量如圖(①所示的一段古城墻的高度,設(shè)計(jì)用平面鏡測(cè)量的示意圖如圖②所示,點(diǎn)P處放一水平的平面鏡,光線(xiàn)從點(diǎn)A出發(fā)經(jīng)過(guò)平面鏡反射后剛好射到古城墻CD的頂端C處。

(1)已知AB⊥BD、CD⊥BD,且測(cè)得AB=1.2m,BP=1.8m.PD=12m,求該城墻的高度(平面鏡的原度忽略不計(jì)):
(2)請(qǐng)你設(shè)計(jì)一個(gè)測(cè)量這段古城墻高度的方案。
要求:①面出示意圖(不要求寫(xiě)畫(huà)法);②寫(xiě)出方案,給出簡(jiǎn)要的計(jì)算過(guò)程:③給出的方案不能用到圖②的方法。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC是等邊三角形,AB=4,E是AC的中點(diǎn),D是直線(xiàn)BC上一動(dòng)點(diǎn),線(xiàn)段ED繞點(diǎn)E逆時(shí)針旋轉(zhuǎn)90°,得到線(xiàn)段EF,當(dāng)點(diǎn)D運(yùn)動(dòng)時(shí),則AF的最小值為( )
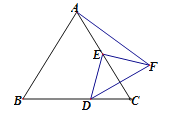
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,以斜邊AB為邊向外作正方形ABDE,且正方形對(duì)角線(xiàn)交于點(diǎn)O,連接OC,已知AC=3,OC=6![]() ,則另一直角邊BC的長(zhǎng)為_____.
,則另一直角邊BC的長(zhǎng)為_____.
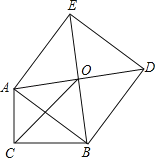
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在Rt△ABC中,D為斜邊AB的中點(diǎn),∠B=60°,BC=2cm,動(dòng)點(diǎn)E從點(diǎn)A出發(fā)沿AB向點(diǎn)B運(yùn)動(dòng),動(dòng)點(diǎn)F從點(diǎn)D出發(fā),沿折線(xiàn)D﹣C﹣B運(yùn)動(dòng),兩點(diǎn)的速度均為1cm/s,到達(dá)終點(diǎn)均停止運(yùn)動(dòng),設(shè)AE的長(zhǎng)為x,△AEF的面積為y,則y與x的圖象大致為( )
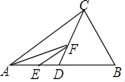
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:點(diǎn)P在△ABC內(nèi),且滿(mǎn)足∠APB=∠APC(如下圖),∠APB+∠BAC=180°,
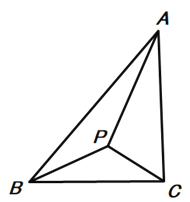
(1)求證:△PAB∽△PCA:
(2)如下圖,如果∠APB=120°,∠ABC=90°求![]() 的值;
的值;
(3)如圖,當(dāng)∠BAC=45°,△ABC為等腰三角形時(shí),求tan∠PBC的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
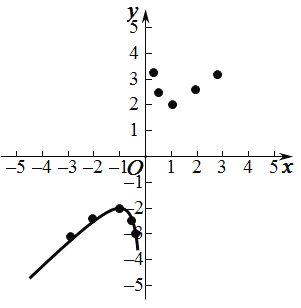
【題目】某“興趣小組”根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),對(duì)函數(shù)y=x+![]() 的圖象和性質(zhì)進(jìn)行了探究,探究過(guò)程如下,請(qǐng)補(bǔ)充完整
的圖象和性質(zhì)進(jìn)行了探究,探究過(guò)程如下,請(qǐng)補(bǔ)充完整
(1)函數(shù)y=x+![]() 的自變量取值范圍是 .
的自變量取值范圍是 .
(2)下表是x與y的幾組對(duì)應(yīng)值

則表中m的值為 .
(3)根據(jù)表中數(shù)據(jù),在如圖所示平面直角坐標(biāo)xOy中描點(diǎn),并畫(huà)出函數(shù)的一部分,請(qǐng)畫(huà)出該函數(shù)的圖象的另一部分,
(4)觀察函數(shù)圖象:寫(xiě)出該函數(shù)的一條性質(zhì): .
(5)進(jìn)一步探究發(fā)現(xiàn):函數(shù)y=x+![]() 圖象與直線(xiàn)y=﹣2只有一交點(diǎn),所以方程x+
圖象與直線(xiàn)y=﹣2只有一交點(diǎn),所以方程x+![]() =﹣2只有1個(gè)實(shí)數(shù)根,若方程x+
=﹣2只有1個(gè)實(shí)數(shù)根,若方程x+![]() =k(x<0)有兩個(gè)不相等的實(shí)數(shù)根,則k的取值范圍是 .
=k(x<0)有兩個(gè)不相等的實(shí)數(shù)根,則k的取值范圍是 .
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com