
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,連接
,連接![]() .
.
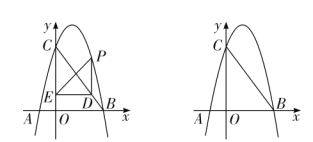
(1)求拋物線的解析式;
(2)點![]() 是拋物線上一點,設
是拋物線上一點,設![]() 點的橫坐標為
點的橫坐標為![]() .
.
①當點![]() 在第一象限時,過點
在第一象限時,過點![]() 作
作![]() 軸,交
軸,交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,連接
,連接![]() ,當
,當![]() 和
和![]() 相似時,求點
相似時,求點![]() 的坐標;
的坐標;
②請直接寫出使![]() 的點
的點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)①點
;(2)①點![]() 的坐標為
的坐標為![]() 或
或![]() ;②點
;②點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
【解析】
(1)將![]() 、
、![]() 兩點坐標代入拋物線
兩點坐標代入拋物線![]() ,列出關于a和b的方程組求解即可;(2)①設
,列出關于a和b的方程組求解即可;(2)①設![]() ,由點
,由點![]() 和點
和點![]() 可得
可得![]() 的表達式,分兩種情況:當
的表達式,分兩種情況:當![]() 時和當
時和當![]() 時根據相似三角形的性質求解即可;
時根據相似三角形的性質求解即可;
②如圖,過點B作∠ABC的角平分線分別交y軸、拋物線于點M、P,在x軸的下方作![]() ,設點M的坐標為(0,k),求出點M的坐標,得出直線BM的解析式,聯立方程,求出點P的坐標,同理可得點
,設點M的坐標為(0,k),求出點M的坐標,得出直線BM的解析式,聯立方程,求出點P的坐標,同理可得點![]() .
.
(1)將![]() 、
、![]() 兩點坐標代入拋物線
兩點坐標代入拋物線![]() 解析式,
解析式,
可得![]() ,解得
,解得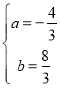 ,
,
∴拋物線的解析式為![]() ;
;
(2)①設![]() ,
,
由點![]() 和點
和點![]() 可得
可得![]() 的表達式:
的表達式:![]() ,
,
![]()
則![]() ,
,
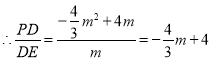 ,
,
![]() 軸,
軸,![]() 軸,
軸,
![]() ,
,
(Ⅰ)當![]() 時,
時,![]() ,
,
則![]() ,
,
![]()
(Ⅱ)當![]() 時,
時,![]() ,
,
則![]() ,
,
![]() ,
,
∴當![]() 與
與![]() 相似時,點
相似時,點![]() 的坐標為
的坐標為![]() 或
或![]() ;
;
②如圖,過點B作∠ABC的角平分線分別交y軸、拋物線于點M、P,在x軸的下方作∠ABP= ![]() ∠ABC,設點M的坐標為(0,k),
∠ABC,設點M的坐標為(0,k),
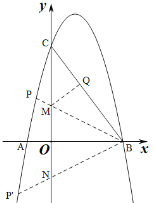
∵OB=3,OC=4,
∴BC=5,
∵BM平分∠ABC,
∴MO=MQ,
∴![]() ,
,
即![]() ,
,
解得![]() ,點M的坐標為(0,
,點M的坐標為(0,![]() ),
),
∴直線BM的解析式為![]() ,
,
聯立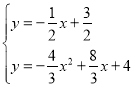 ,
,
解得![]() 或
或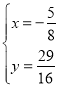 ,
,
∴點P的坐標為![]() ,
,
由作圖可知,M與點N關于x軸對稱,
∴點N的坐標為(0,![]() ),
),
同理可得點![]() 的坐標為
的坐標為![]() ,
,
綜上點P的坐標為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】【探究證明】
(1)某班數學課題學習小組對矩形內兩條互相垂直的線段與矩形兩鄰邊的數量關系進行探究,提出下列問題,請你給出證明.
如圖①,在矩形ABCD中,EF⊥GH,EF分別交AB,CD于點E,F,GH分別交AD,BC于點G,H.求證: ![]() ;
;
【結論應用】
(2)如圖②,在滿足(1)的條件下,又AM⊥BN,點M,N分別在邊BC,CD上,若![]() ,則
,則![]() 的值為 ;
的值為 ;
【聯系拓展】
(3)如圖③,四邊形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,點M,N分別在邊BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
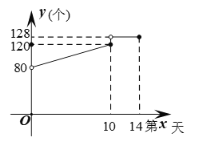
【題目】某廠家接到一批特殊產品的生產訂單,客戶要求在兩周內完成生產,并商定這批產品的出廠價為每個16元.受市場影響,制造這批產品的某種原材料成本價持續上漲,設第x天(1≤x≤14,且x為整數)每個產品的成本為m元,m與x之間的函數關系為m=![]() x+8.訂單完成后,經統計發現工人王師傅第x天生產的產品個數y與x滿足如圖所示的函數關系:
x+8.訂單完成后,經統計發現工人王師傅第x天生產的產品個數y與x滿足如圖所示的函數關系:
(1)寫出y與x之間的函數關系式及自變量x的取值范圍;
(2)設王師傅第x天創造的產品利潤為W元,問王師傅第幾天創造的利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 和點
和點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,點
,點![]() 是拋物線的頂點,過點
是拋物線的頂點,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,連接
,連接![]() .
.
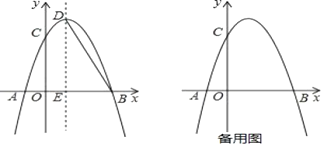
(1)求拋物線的解析式及點![]() 的坐標;
的坐標;
(2)點![]() 是拋物線上的動點,當
是拋物線上的動點,當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(3)若點![]() 是
是![]() 軸上方拋物線上的動點,以
軸上方拋物線上的動點,以![]() 為邊作正方形
為邊作正方形![]() ,隨著點
,隨著點![]() 的運動,正方形的大小、位置也隨著改變,當頂點
的運動,正方形的大小、位置也隨著改變,當頂點![]() 或
或![]() 恰好落在
恰好落在![]() 軸上時,請直接寫出點
軸上時,請直接寫出點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若拋物線![]() 與
與![]() 軸兩個交點間的距離為2,稱此拋物線為定弦拋物線,已知某定弦拋物線的對稱軸為直線
軸兩個交點間的距離為2,稱此拋物線為定弦拋物線,已知某定弦拋物線的對稱軸為直線![]() ,將此拋物線向左平移2個單位,再向下平移3個單位,得到的拋物線過點( )
,將此拋物線向左平移2個單位,再向下平移3個單位,得到的拋物線過點( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】周末,小明與小亮兩個人打算騎共享單車騎行出游,兩人打開手機APP進行選擇,已知附近共有3種品牌的5輛車,其中A品牌與B品牌各有2輛,C品牌有1輛,手機上無法識別品牌,且有人選中車后其他人無法再選.
(1)若小明首先選擇,則小明選中A品牌單車的概率為 ;
(2)求小明和小亮選中同一品牌單車的概率.(請用“畫樹狀圖”或“列表”的方法給出分析過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD和正方形EFGH的對角線BD,EG都在直線l上,將正方形ABCD沿著直線l從點D與點E重合開始向右平移,直到點B與點G重合為止,設點D平移的距離為x,![]() ,
,![]() ,兩個正方形重合部分的面積為S,則S關于x的函數圖象大致為( )
,兩個正方形重合部分的面積為S,則S關于x的函數圖象大致為( )
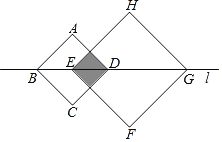
A.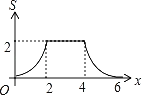 B.
B.
C.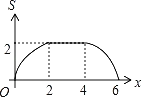 D.
D.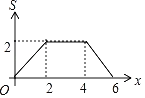
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校隨機抽查了部分九年級女生進行1分鐘仰臥起坐測試,并將測試的結果繪制成了如圖的不完整的統計表和頻數分布直方圖(注:在頻數分布直方圖中,每組含左端點,但不含右端點):
仰臥起坐次數的范圍(次) | 15~20 | 20~25 | 25~30 | 30~35 |
頻數 | 3 | 10 | 12 |
|
頻率 |
|
|
|
|

(1)30~35的頻數是 、25~30的頻率是 .并把統計圖補充完整;
(2)被抽查的所有女同學仰臥起坐次數的中位數是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com