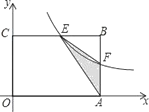
【題目】如圖，在矩形OABC中，OA=6，OC=4，F是AB上的一個動點（F不與A，B重合），過點F的反比例函數
的圖象與BC邊交于點E.
（1）當F為AB的中點時，求該函數的解析式；
（2）當k為何值時，△EFA的面積最大，最大面積是多少？
【答案】（1）該函數的解析式為y=
（x＞0）；（2）當k=12時，S有最大值，S最大=3.
【解析】如圖，在矩形OABC中，OA=6，OC=4，F是AB上的一個動點（F不與A，B重合），過點F的反比例函數
(k>0) 的圖象與BC邊交于點E.
（1）當F為AB的中點時，求該函數的解析式；
（2）當k為何值時，△EFA的面積最大，最大面積是多少？
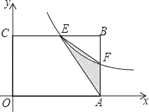
試題分析：（1）當F為AB的中點時，點F的坐標為（3，1），由此代入求得函數解析式即可；
（2）根據圖中的點的坐標表示出三角形的面積，得到關于k的二次函數，利用二次函數求出最值即可．
試題解析：（1）∵在矩形OABC中，OA=6，OC=4，∴B（6，4），
∵F為AB的中點，∴F（6，2），
又∵點F在反比例函數
（k＞0）的圖象上，∴k=12，
∴該函數的解析式為y=
（x＞0）
（2）由題意知E，F兩點坐標分別為E（
，4），F（6， 
），
∴
，
=
=
=
=
，
∴當k=12時，S有最大值．S最大=3．
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝2，AC＝
，∠BAC＝105°，△ABD，△ACE，△BCF都是等邊三角形，則四邊形AEFD的面積為__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知點O為數軸原點，點A在數軸上對應的數為a，點B對應的數為b，A、B之間的距離記作AB，且|a+4|+（b﹣10）2＝0．
（1）求線段AB的長；
（2）設點P在數軸上對應的數為x，當PA+PB＝20時，求x的值；
（3）如圖，M、N兩點分別從O、B出發以v1、v2的速度同時沿數軸負方向運動（M在線段AO上，N在線段BO上），P是線段AN的中點，若M、N運動到任一時刻時，總有PM為定值，下列結論：①
的值不變；②v1+v2的值不變．其中只有一個結論是正確的，請你找出正確的結論并求值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某班一次數學測試成績如下：
63, 84, 91, 53, 69, 81, 57, 69, 91, 78，
75, 81, 80, 67, 76, 81, 79, 94, 61, 69，
89, 70, 70, 87, 81, 86, 90, 88, 85, 67.
補充完整頻數分布表：
成績 |
|
|
|
|
|
頻數 |
（2）補充完整圖中的頻數分布直方圖：
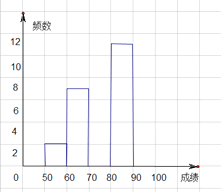
（3）若80分以上（含80分）的成績為優秀，那么該班這次數學測驗的優秀率是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
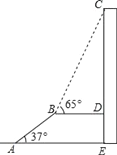
【題目】如圖，AB是長為10m，傾斜角為37°的自動扶梯，平臺BD與大樓CE垂直，且與扶梯AB的長度相等，在B處測得大樓頂部C的仰角為65°，求大樓CE的高度（結果保留整數）.
（參考數據：sin37°≈
，tan37°≈
，sin65°≈
，tan65°≈
）
查看答案和解析>>
科目：初中數學 來源： 題型：
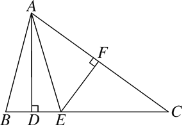
【題目】如圖，△ABC中，AD⊥BC于點D，EF垂直平分AC，交AC于點F，交BC于點E，且BD＝DE，連接AE.
(1)若∠BAE＝30°，求∠C的度數；
(2)若△ABC的周長為13cm，AC＝6cm，求DC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】平面直角坐標系xOy中（如圖），已知拋物線y=ax2+bx+3與y軸相交于點C，與x軸正半軸相交于點A，OA=OC，與x軸的另一個交點為B，對稱軸是直線x=1，頂點為P．
（1）求這條拋物線的表達式和頂點P的坐標；
（2）拋物線的對稱軸與x軸相交于點M，求∠PMC的正切值；
（3）點Q在y軸上，且△BCQ與△CMP相似，求點Q的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2019年3月25日是第二十四個“全國中小學生安全教育日”，某校為加強學生的安全意識，以“防火、防溺水、防食物中毒、防校園欺凌”為主題組織了全校學生參加安全知識競賽，從中抽取了部分學生成績（得分為正整數，滿分為100分）進行統計，繪制了兩幅不完整的統計圖，如圖所示.
（1）學校共抽取了______名學生，
_____，n=______.
（2）補全頻數直方圖；
（3）該校共有2000名學生。若成績在70分以下（含70分）的學生安全意識不強，有待進一步加強安全教育，則該校安全意識不強的學生約有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知Rt△OAB，∠OAB＝90°，∠ABO＝30°，斜邊OB＝4，將Rt△OAB繞點O順時針旋轉60°，點D與點A為對應點，畫出Rt△ODC，并連接BC．
（1）填空：∠OBC＝_____°；
（2）如圖，連接AC，作OP⊥AC，垂足為P，求OP的長度是_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
