【題目】已知二次函數
的部分圖象如圖，頂點是
．
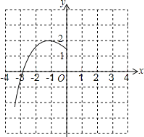
（1）求二次函數的解析式；
（2）若拋物線上兩點
、
的橫坐標滿足
，則
________
；（用“
”、“
”或“
”填空）
（3）觀察圖象，直接寫出當
時，
的取值范圍．
【答案】（1）y=
；（2）
；（3）
【解析】
（1）設二次函數頂點式解析式為y=a（x+1）2+2，然后把點（﹣3，0）代入求出a的值，即可得解；
（2）根據x＜﹣1時，y隨x的增大而減小解答；
（3）根據二次函數的對稱性求出拋物線與x軸的另一交點，然后寫出x軸上方部分的x的取值范圍即可．
（1）∵頂點是（﹣1，2），∴設二次函數頂點式解析式為y=a（x+1）2+2，由圖可知，函數圖象經過點（﹣3，0），∴a（﹣3+1）2+2=0，解得：a=﹣
，∴二次函數的解析式為y=﹣（x+1）2+2，即y=；
（2）∵a=﹣＜0，二次函數圖象對稱軸為直線x=﹣1，∴x＞﹣1時，y隨x的增大而減小，∴﹣1＜x1＜x2時，y1＞y2．
故答案為：＞；
（3）∵函數圖象經過（﹣3，0），對稱軸為直線x=﹣1，∴二次函數與x軸的另一交點坐標為（1，0），∴y＞0時，x的取值范圍﹣3＜x＜1．
科目：初中數學 來源： 題型：
【題目】如圖，一個商人要建一個矩形的倉庫，倉庫的兩邊是住房墻，另外兩邊用
長的建筑材料圍成，且倉庫的面積為
．
求這矩形倉庫的長；
有規格為
和
（單位：
）的地板磚單價分別為
元/塊和
元/塊，若只選其中一種地板磚都恰好能鋪滿倉庫的矩形地面（不計縫隙），用哪一種規格的地板磚費用較少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，
中，
，
于
，
平分
，且
于
，與
相交于點
，
是
邊的中點，連接
與相交于點
，下列結論正確的有( )個
①
；②
；③
；④
是等腰三角形；⑤
.
A.
個B.
個C.
個D.
個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一次函數
的圖象經過點
，且與二次函數
的圖象相交于
、
兩點．
（1）求這兩個函數的表達式及點的坐標；
（2）在同一坐標系中畫出這兩個函數的圖象，并根據圖象回答：當
取何值時，一次函數的函數值小于二次函數的函數值；
（3）求△BOC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面是某同學對多項式（x2﹣4x+2）（x2﹣4x+6）+4進行因式分解的過程
解：設x2﹣4x＝y，
原式＝（y+2）（y+6）+4 （第一步）
＝y2+8y+16 （第二步）
＝（y+4）2（第三步）
＝（x2﹣4x+4）2（第四步）
（1）該同學第二步到第三步運用了因式分解的 （填序號）．
A．提取公因式 B．平方差公式
C．兩數和的完全平方公式 D．兩數差的完全平方公式
（2）該同學在第四步將y用所設中的x的代數式代換，得到因式分解的最后結果．這個結果是否分解到最后？ ．（填“是”或“否”）如果否，直接寫出最后的結果 ．
（3）請你模仿以上方法嘗試對多項式（x2﹣2x）（x2﹣2x+2）+1進行因式分解．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知
、
兩地之間有一條270千米的公路，甲、乙兩車同時出發，甲車以每小時60千米/時的速度沿此公路從地勻速開往地，乙車從地沿此公路勻速開往地，兩車分別到達目的地后停止甲、乙兩車相距的路程
(千米)與甲車的行駛時間
(時)之間的函數關系如圖所示：
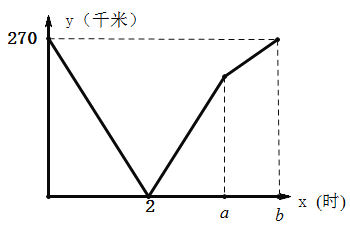
(1)乙年的速度為______千米/時，
_____，
______.
(2)求甲、乙兩車相遇后與之間的函數關系式，并寫出相應的自變量的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場一種商品的進價為每件30元，售價為每件40元．每天可以銷售48件，為盡快減少庫存，商場決定降價促銷．
（1）若該商品連續兩次下調相同的百分率后售價降至每件32.4元，求兩次下降的百分率；
（2）經調查，若每降價0.5元，每天可多銷售4件，那么每天要想獲得510元的利潤，每件應降價多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
