
【題目】銳角△ABC中,BC=6,![]() ,兩動點M,N分別在邊AB,AC上滑動,且MN∥BC,以MN為邊向下作正方形MPQN,設其邊長為x,正方形MPQN與△ABC公共部分的面積為y(y>0).
,兩動點M,N分別在邊AB,AC上滑動,且MN∥BC,以MN為邊向下作正方形MPQN,設其邊長為x,正方形MPQN與△ABC公共部分的面積為y(y>0).
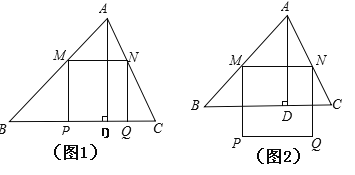
(1)求△ABC中邊BC上高AD;
(2)當x為何值時,PQ恰好落在邊BC上(如圖1);
(3)當PQ在△ABC外部時(如圖2),求y關于x的函數關系式(注明x的取值范圍),并求出x為何值時y最大,最大值是多少?
【答案】(1)4;(2)2.4(或![]() );(3)3,6.
);(3)3,6.
【解析】
(1)利用三角形的面積公式容易得出△ABC中邊BC上高AD的長度.
(2)因為正方形的位置在變化,但是△AMN∽△ABC沒有改變,利用相似三角形對應邊上高的比等于相似比,得出等量關系,代入解析式可得出;
(3)用含x的式子表示矩形MEFN邊長,從而求出面積的表達式,配方成頂點式可得解.
解:(1)由BC=6,S△ABC=12,得AD=4;
(2)當PQ恰好落在邊BC上時,
∵MN∥BC,
∴△AMN∽△ABC.
![]()
即![]() ;
;
(3)設BC分別交MP,NQ于E,F,則四邊形MEFN為矩形.
設ME=NF=h,AD交MN于G(如圖2)GD=NF=h,AG=4-h.
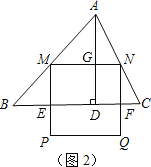
∵MN∥BC,
∴△AMN∽△ABC.
![]() 即
即![]() ,
,
![]() ,
,
![]() ,
,
配方得:![]()
∴當x=3時,y有最大值,最大值是6.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的對角線上的兩個動點M、N,滿足AB=![]() MN,點P是BC的中點,連接AN、PM,若AB=6,則當AN+PM取最小值時,線段AN的長度為( )
MN,點P是BC的中點,連接AN、PM,若AB=6,則當AN+PM取最小值時,線段AN的長度為( )
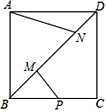
A.4B.2![]() C.6D.3
C.6D.3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=﹣2,與x軸的一個交點在(﹣3,0)和(﹣4,0)之間,其部分圖象如圖所示則下列結論:①4a﹣b=0;②c<0;③c>3a;④4a﹣2b>at2+bt(t為實數);⑤點(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() )是該拋物線上的點,則y2<y1<y3,其中,正確結論的個數是( )
)是該拋物線上的點,則y2<y1<y3,其中,正確結論的個數是( )
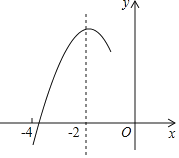
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
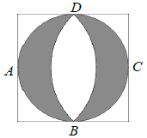
【題目】文藝復興時期,意大利藝術大師達芬奇曾研究過圓弧所圍成的許多圖形的面積問題. 如圖所示稱為達芬奇的“貓眼”,可看成圓與正方形的各邊均相切,切點分別為![]() ,
,![]() 所在圓的圓心為點
所在圓的圓心為點![]() (或
(或![]() ). 若正方形的邊長為2,則圖中陰影部分的面積為( )
). 若正方形的邊長為2,則圖中陰影部分的面積為( )
A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
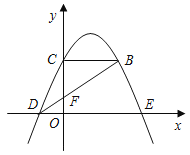
【題目】如圖,拋物線y=﹣![]() (x﹣k)2+
(x﹣k)2+![]() 經過點D(﹣1,0),與x軸正半軸交于點E,與y軸交于點C,過點C作CB∥x軸交拋物線于點B.連接BD交y軸于點F.
經過點D(﹣1,0),與x軸正半軸交于點E,與y軸交于點C,過點C作CB∥x軸交拋物線于點B.連接BD交y軸于點F.
(1)求點E的坐標.
(2)求△CFB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
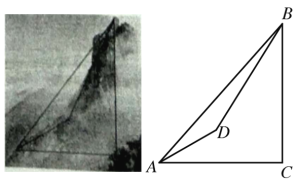
【題目】某學校數學興趣小組想利用數學知識測量某座山的海拔高度,如圖,他們在山腰A處測得山頂B的仰角為45°,他們從A處沿著坡度為i=1 : ![]() 的斜坡前進1000 m到達D處,在D處測得山頂B的仰角為58°,若點A處的海拔為12米,求該座山頂點B處的海拔高度,(結果保留整數,參考數據:tan 58°≈1.60,sin 58°≈0. 85,cos 58°≈0.53,
的斜坡前進1000 m到達D處,在D處測得山頂B的仰角為58°,若點A處的海拔為12米,求該座山頂點B處的海拔高度,(結果保留整數,參考數據:tan 58°≈1.60,sin 58°≈0. 85,cos 58°≈0.53,![]() ≈1. 732)
≈1. 732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為豐富學生的校園生活,準備從體育用品商店一次性購買若干個足球和籃球(每個足球的價格相同,每個籃球的價格相同),若購買3個足球和2個籃球共需310元,購買2個足球和5個籃球共需500元。
(1)求購買一個足球、一個籃球各需多少元?
(2)根據學校實際情況,需從體育用品商店一次性購買足球和籃球共96個,要求購買足球和籃球的總費用不超過5720元,這所中學最多可以購買多少個籃球?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com