
【題目】如圖,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點(diǎn),
的中點(diǎn),![]() 點(diǎn)在邊
點(diǎn)在邊![]() 上,連接
上,連接![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 的垂線交
的垂線交![]() 于點(diǎn)
于點(diǎn)![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() ,且
,且![]() 與四邊形
與四邊形![]() 的周長(zhǎng)相等,設(shè)
的周長(zhǎng)相等,設(shè)![]() ,
,![]() .
.
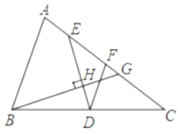
(1)求證:![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)見解析;(2)![]()
【解析】
(1)根據(jù)中位線的性質(zhì)和定義得DF =![]() c,CF=
c,CF=![]() b,結(jié)合△CDE與四邊形ABDE的周長(zhǎng)相等,得到CE=
b,結(jié)合△CDE與四邊形ABDE的周長(zhǎng)相等,得到CE=![]() ,可得EF的長(zhǎng),進(jìn)而即可得到結(jié)論;
,可得EF的長(zhǎng),進(jìn)而即可得到結(jié)論;
(2)連接BE,DG,過點(diǎn)A作AP⊥BG于P,過B作BM⊥DG于M,過E作EN⊥DG于N,證明四邊形BMNE是平行四邊形,易得BE∥DG,從而得到△ABE∽△FDG,進(jìn)而得到FG=![]() (bc),再證∠BAP=∠DEF=∠PAC,得到△ABP≌△AGP,從而得AB=AG=c,結(jié)合CF=FG+CG,得到關(guān)于b,c的等式,即可得到結(jié)論.
(bc),再證∠BAP=∠DEF=∠PAC,得到△ABP≌△AGP,從而得AB=AG=c,結(jié)合CF=FG+CG,得到關(guān)于b,c的等式,即可得到結(jié)論.
(1)證明:∵點(diǎn)![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點(diǎn),
的中點(diǎn),
∴![]() 是
是![]() 的中位線,
的中位線,
∴![]() ,
,![]() .
.
∵點(diǎn)![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),
∴![]() .
.
∵![]() 與四邊形
與四邊形![]() 的周長(zhǎng)相等,
的周長(zhǎng)相等,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)解:連接![]() ,
,![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于
于![]() ,過B作BM⊥DG于M,過E作EN⊥DG于N,如圖所示.
,過B作BM⊥DG于M,過E作EN⊥DG于N,如圖所示.

∵![]() ,
,
∴![]()
∴![]() ,
,
∵△BDG和△EDG的底邊為DG,
∴底邊DG上的高BM=EN.
∵BM⊥DG,EN⊥DG,
∴BM∥EN,
∴四邊形BMNE是平行四邊形,
∴BE∥DG.
∵![]() 是
是![]() 的中位線,
的中位線,
∴![]() ,
,![]() ,
,
∴∠BAE=∠DFG.
∵BE∥DG,
∴∠AEB=∠FGD,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴∠BAE=∠DFG=2∠DEF,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴∠APB=∠APG=90°.
∵AP=AP,
∴△ABP≌△AGP,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
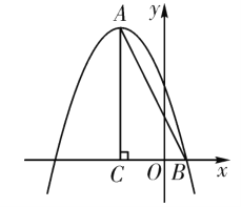
【題目】如圖1,已知拋物線![]() 與x軸相交于A、B兩點(diǎn)(A左B右),與y軸交于點(diǎn)C.其頂點(diǎn)為D.
與x軸相交于A、B兩點(diǎn)(A左B右),與y軸交于點(diǎn)C.其頂點(diǎn)為D.
(1)求點(diǎn)D的坐標(biāo)和直線BC對(duì)應(yīng)的一次函數(shù)關(guān)系式;
(2)若正方形PQMN的一邊PQ在線段AB上,另兩個(gè)頂點(diǎn)M、N分別在BC、AC上,試求M、N兩點(diǎn)的坐標(biāo);
(3)如圖1,E是線段BC上的動(dòng)點(diǎn),過點(diǎn)E作DE的垂線交BD于點(diǎn)F,求DF的最小值.
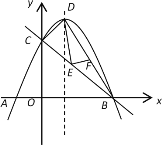
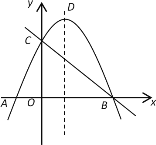
(圖1) (圖2)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明和小剛一起做游戲,游戲規(guī)則如下:將分別標(biāo)有數(shù)字 1, 2, 3, 4 的 4 個(gè)小球放入一個(gè)不透明的袋子中,這些球除數(shù)字外都相同.從中隨機(jī)摸出一個(gè)球記下數(shù)字后放回,再?gòu)闹须S機(jī)摸出一個(gè)球記下數(shù)字.若兩次數(shù)字差的絕對(duì)值小于 2,則小明獲勝,否則小剛獲勝.這個(gè)游戲?qū)扇斯絾幔空?qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,直線y=x-1交x軸、y軸于A、B點(diǎn),點(diǎn)P(1,![]() ,且S四邊形PAOB=3.5,雙曲線y=
,且S四邊形PAOB=3.5,雙曲線y=![]() 經(jīng)過點(diǎn)P.
經(jīng)過點(diǎn)P.
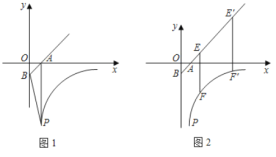
(1)求k的值;
(2)如圖2,直線![]() )交射線BA于E,交雙曲線y=
)交射線BA于E,交雙曲線y=![]() 于F,將直線
于F,將直線![]() 向右平移4個(gè)單位長(zhǎng)度后交射線于
向右平移4個(gè)單位長(zhǎng)度后交射線于![]() ,交雙曲線y=
,交雙曲線y=![]() 于
于![]() ,若
,若![]()
![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
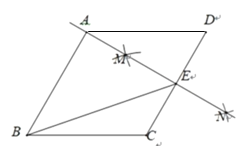
【題目】如圖,在菱形ABCD中,按以下步驟作圖:
①分別以點(diǎn)C和點(diǎn)D為圓心,大于![]() 的同樣的長(zhǎng)為半徑作弧,兩弧交于M,N兩點(diǎn);
的同樣的長(zhǎng)為半徑作弧,兩弧交于M,N兩點(diǎn);
②作直線MN,交CD于點(diǎn)E,連接BE.
若直線MN恰好經(jīng)過點(diǎn)A,則下列說法錯(cuò)誤的是( )
A.ABC60°
B.![]()
C.若AB4,則BE![]()
D.tanCBE![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
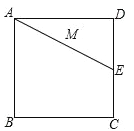
【題目】如果,正方形ABCD的邊長(zhǎng)為2cm,E為CD邊上一點(diǎn),∠DAE=30°,M為AE的中點(diǎn),過點(diǎn)M作直線分別與AD、BC相交于點(diǎn)P、Q,若PQ=AE,則PD等于( )
A.![]() cm或
cm或![]() cm B.
cm B.![]() cm C.
cm C.![]() cm或
cm或![]() cm D.
cm D.![]() cm或
cm或![]() cm
cm
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商店銷售![]() 型和
型和![]() 型兩種學(xué)習(xí)機(jī),其中用10000元采購(gòu)
型兩種學(xué)習(xí)機(jī),其中用10000元采購(gòu)![]() 型學(xué)習(xí)機(jī)臺(tái)數(shù)和用8000元采購(gòu)
型學(xué)習(xí)機(jī)臺(tái)數(shù)和用8000元采購(gòu)![]() 型學(xué)習(xí)機(jī)臺(tái)數(shù)相等,且一臺(tái)
型學(xué)習(xí)機(jī)臺(tái)數(shù)相等,且一臺(tái)![]() 型學(xué)習(xí)機(jī)比一臺(tái)
型學(xué)習(xí)機(jī)比一臺(tái)![]() 型學(xué)習(xí)機(jī)進(jìn)價(jià)多100元.
型學(xué)習(xí)機(jī)進(jìn)價(jià)多100元.
(1)求一臺(tái)![]() 型和
型和![]() 型學(xué)習(xí)機(jī)價(jià)格各是多少元?
型學(xué)習(xí)機(jī)價(jià)格各是多少元?
(2)若購(gòu)進(jìn)![]() 型學(xué)習(xí)機(jī)共100臺(tái),其中
型學(xué)習(xí)機(jī)共100臺(tái),其中![]() 型的進(jìn)貨量不超過
型的進(jìn)貨量不超過![]() 型的2倍,設(shè)購(gòu)進(jìn)
型的2倍,設(shè)購(gòu)進(jìn)![]() 型學(xué)習(xí)機(jī)
型學(xué)習(xí)機(jī)![]() 臺(tái).
臺(tái).
①求![]() 的取值范圍.
的取值范圍.
②已知![]() 型學(xué)習(xí)機(jī)售價(jià)均是900元/臺(tái),實(shí)際進(jìn)貨時(shí),廠家對(duì)
型學(xué)習(xí)機(jī)售價(jià)均是900元/臺(tái),實(shí)際進(jìn)貨時(shí),廠家對(duì)![]() 型學(xué)習(xí)機(jī)在原進(jìn)貨價(jià)的基礎(chǔ),上下調(diào)
型學(xué)習(xí)機(jī)在原進(jìn)貨價(jià)的基礎(chǔ),上下調(diào)![]() 元,且限定商店最多購(gòu)進(jìn)
元,且限定商店最多購(gòu)進(jìn)![]() 型學(xué)習(xí)機(jī)60臺(tái),若商店保持同種學(xué)習(xí)機(jī)的售價(jià)不變,請(qǐng)你根據(jù)以上信息,求出使這100臺(tái)學(xué)習(xí)機(jī)銷售總利潤(rùn)
型學(xué)習(xí)機(jī)60臺(tái),若商店保持同種學(xué)習(xí)機(jī)的售價(jià)不變,請(qǐng)你根據(jù)以上信息,求出使這100臺(tái)學(xué)習(xí)機(jī)銷售總利潤(rùn)![]() (元)的最大值.
(元)的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,在四邊形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,點(diǎn)E,F分別是BC,AD的中點(diǎn).
,點(diǎn)E,F分別是BC,AD的中點(diǎn).
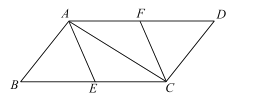
(1)求證:![]() ;
;
(2)當(dāng)![]() 與
與![]() 滿足什么數(shù)量關(guān)系時(shí),四邊形
滿足什么數(shù)量關(guān)系時(shí),四邊形![]() 是正方形?請(qǐng)證明.
是正方形?請(qǐng)證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,拋物線
,拋物線![]() 經(jīng)過
經(jīng)過![]() 兩點(diǎn).
兩點(diǎn).
(1)求拋物線的解析式;
(2)點(diǎn)![]() 是直線
是直線![]() 上方拋物線上的一點(diǎn),過點(diǎn)
上方拋物線上的一點(diǎn),過點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,交線段
,交線段![]() 于點(diǎn)
于點(diǎn)![]() ,使
,使![]() .
.
①求點(diǎn)![]() 的坐標(biāo)和
的坐標(biāo)和![]() 的面積;
的面積;
②在直線![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使
,使![]() 為直角三角形?若存在,直接寫出符合條件的所有點(diǎn)
為直角三角形?若存在,直接寫出符合條件的所有點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說明理由.
的坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com