
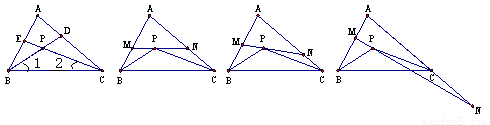
如圖①,△ABC的角平分線BD、CE相交于點P.
(1)如果∠A=70°,求∠BPC的度數;
(2)如圖②,過P點作直線MN∥BC,分別交AB和AC于點M和N,試求∠MPB+∠NPC的度數(用含∠A的代數式表示);
① ② ③ ④
在(2)的條件下,將直線MN繞點P旋轉.
(ⅰ)當直線MN與AB、AC的交點仍分別在線段AB和AC上時,如圖③,試探索∠MPB、∠NPC、∠A三者之間的數量關系,并說明你的理由;
(ⅱ)當直線MN與AB的交點仍在線段AB上,而與AC的交點在AC的延長線上時,如圖④,試問(ⅰ)中∠MPB、∠NPC、∠A三者之間的數量關系是否仍然成立?若成立,請說明你的理由;若不成立,請給出∠MPB、∠NPC、∠A三者之間的數量關系,并說明你的理由.
(1)125°;(2)∠MPB+∠NPC=90°- ∠A;(3)∠MPB+∠NPC= 90°-
∠A;(3)∠MPB+∠NPC= 90°- ∠A,∠MPB-∠NPC=90°-
∠A,∠MPB-∠NPC=90°- ∠A.
∠A.
【解析】
試題分析:(1)由三角形內角和定理可知∠ABC+∠ACB=180°-∠A,由角平分線的性質可知及三角形內角和定理可求出∠BPC的度數;
(2)利用平行線的性質求解或先說明∠BPC=90°+ ∠A;
∠A;
(3)(ⅰ)先說明∠BPC=90°+ ∠A,則∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A,則∠MPB+∠NPC=180°-∠BPC=180°-(90°+ ∠A)= 90°-
∠A)= 90°- ∠A;(ⅱ)不成立,∠MPB-∠NPC=90°-
∠A;(ⅱ)不成立,∠MPB-∠NPC=90°- ∠A.理由:由圖可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+
∠A.理由:由圖可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+ ∠A,因此∠MPB-∠NPC=180°-∠BPC=180°-(90°+
∠A,因此∠MPB-∠NPC=180°-∠BPC=180°-(90°+ ∠A)= 90°-
∠A)= 90°- ∠A.
∠A.
試題解析::(1)∵在△ABC中,∠A+∠B+∠ACB=180°,
∵∠A=70°,
∴∠ABC+∠ACB=110°,
∵∠1=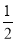 ∠ABC,
∠ABC,
∠2=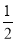 ∠ACB,
∠ACB,
∴∠1+∠2=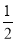 (∠ABC+∠ACB)
(∠ABC+∠ACB)
=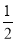 ×110°=55°,
×110°=55°,
∴∠BPC=180°-(∠1+∠2)=180°-55°=125°;
(2)由(1)可證∠BPC=90°+ ∠A,
∠A,
∴∠MPB+∠NPC=180°-∠BPC=180°-(90°+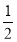 ∠A)=90°-
∠A)=90°- ∠A;
∠A;
(3)(ⅰ)∠MPB+∠NPC= 90°- ∠A.
∠A.
理由:先說明∠BPC=90°+ ∠A,則∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A,則∠MPB+∠NPC=180°-∠BPC=180°-(90°+ ∠A)= 90°-
∠A)= 90°- ∠A;
∠A;
(ⅱ)不成立(1分),∠MPB-∠NPC=90°- ∠A(1分).
∠A(1分).
理由:由圖可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+ ∠A,
∠A,
∴∠MPB-∠NPC=180°-∠BPC=180°-(90°+ ∠A)= 90°-
∠A)= 90°- ∠A.
∠A.
考點: (1)平行線的性質;2.角平分線的性質;3.三角形內角和.


科目:初中數學 來源:2016屆江蘇省南京市高淳區七年級下學期期中考試數學試卷(解析版) 題型:選擇題
如圖,點 在
在 的延長線上,下列條件中能判斷AB//CD的是( )
的延長線上,下列條件中能判斷AB//CD的是( )
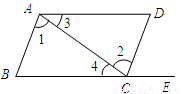
A.∠3=∠4 B.∠D=∠DCE
C.∠B=∠D D.∠1=∠2
查看答案和解析>>
科目:初中數學 來源:2016屆江蘇泰興楚水實驗中學七年級下學期第一次調研數學卷(解析版) 題型:解答題
如圖,BD是△ABC的角平分線,DE∥BC,交AB于點E,∠A=45°,∠BDC=60°。

(1)求∠C的度數;
(2)求∠BED的度數.
查看答案和解析>>
科目:初中數學 來源:2016屆江蘇無錫市七年級下學期期中考試數學卷(解析版) 題型:選擇題
為求1+2+22+23+…+22008的值,可令S=1+2+22+23+…+22008,則2S=2+22+23+24+…+22009,因此2S-S=22009-1,所以1+2+22+23+…+22008=22009-1.仿照以上推理計算出1+3+32+33+…+32014的值是( )
A.32015-1 B.32014-1 C.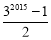 D.
D.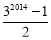
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com