
【題目】如圖,![]() ,
,![]() ,反比例函數(shù)
,反比例函數(shù)![]() (
(![]() )過點
)過點![]() ,
,![]() (
(![]() )的圖象分別過點
)的圖象分別過點![]() 、
、![]() ,直線BC交y軸于點D,
,直線BC交y軸于點D,![]() ∥
∥![]() 軸.
軸.
(1)求![]() 和
和![]() 的值;
的值;
(2)求![]() 的面積.
的面積.
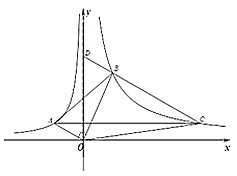
【答案】(1)1,8;(2)20
【解析】
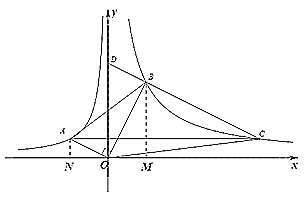
(1)把點A的坐標(biāo)代入![]() 即可求得a的值,作
即可求得a的值,作![]() ⊥
⊥![]() 軸于
軸于![]() ,作
,作![]() ⊥
⊥![]() 軸于
軸于![]() ,證得
,證得![]() ,根據(jù)
,根據(jù)![]() ,得到相似比,再利用反比例函數(shù)k的幾何意義,求得答案;
,得到相似比,再利用反比例函數(shù)k的幾何意義,求得答案;
(2)先分別求得點C、B的坐標(biāo),利用待定系數(shù)法求得直線BC的解析式,求得點D的坐標(biāo),再用三角形面積公式即可求得答案.
(1)∵點![]() 在
在![]() 上,
上,
∴![]() ,
,![]() ,
,
過點A作![]() ⊥
⊥![]() 軸于
軸于![]() ,作
,作![]() ⊥
⊥![]() 軸于
軸于![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
根據(jù)反比例函數(shù)![]() 中k值的幾何意義知:
中k值的幾何意義知:![]() ,
,
故:![]() ,
,![]() ;
;
(2)∵![]() ∥
∥![]() 軸,點C在
軸,點C在![]() 上,
上,
∴點A、C的縱坐標(biāo)相同,![]() ,
,
∴點C的坐標(biāo)為:![]() ,
,
由(1)知:![]() ,
,![]()
又![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴點B的坐標(biāo)為:![]() ,
,
設(shè)直線BC的解析式為:![]() ,
,
∴![]() ,
,
解得: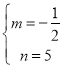 ,
,
∴直線BC的解析式為:![]() ,
,
令![]() ,則
,則![]() ,
,
∴點D的坐標(biāo)為:![]() ,
,
∴![]() .
.


 培優(yōu)三好生系列答案
培優(yōu)三好生系列答案 優(yōu)化作業(yè)上海科技文獻出版社系列答案
優(yōu)化作業(yè)上海科技文獻出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形網(wǎng)格中的每個小正方形的邊長都是1,每個小正方形的頂點叫做格點.△ABC的三個頂點A,B,C都在格點上.將△ABC繞點A按順時針方向旋轉(zhuǎn)90°得到△AB′C′.
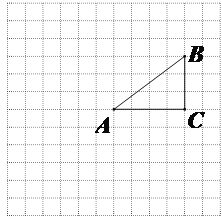
(1)在正方形網(wǎng)格中,畫出△AB′C′;
(2)計算線段AB在變換到AB′的過程中掃過的區(qū)域的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
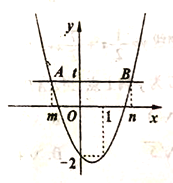
【題目】已知二次函數(shù)![]() 的圖象如圖所示,對于下列結(jié)論:①
的圖象如圖所示,對于下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤方程
;⑤方程![]() 的根是
的根是![]() ,
,![]() ,其中正確結(jié)論的個數(shù)是( )
,其中正確結(jié)論的個數(shù)是( )
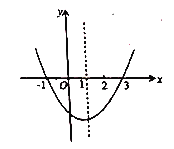
A.5B.4C.3D.2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC與BD交于點O.過點C作BD的平行線,過點D作AC的平行線,兩直線相交于點E.
(1)求證:四邊形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面積是 .

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中2條直線,分別為![]()
![]() ,
,![]()
![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 軸的平行線交
軸的平行線交![]() 于點
于點![]() ,拋物線
,拋物線![]() 過
過![]() 、
、![]() 、
、![]() 三點.
三點.
下列判斷中:
①![]() ;
;
②拋物線關(guān)于直線![]() 軸對稱 ;
軸對稱 ;
③點![]() 在拋物線上方;
在拋物線上方;
④![]() ;
;
⑤![]() .其中正確的個數(shù)有( )
.其中正確的個數(shù)有( )
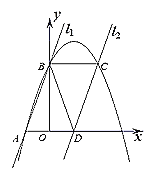
A.5B.4C.3D.2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
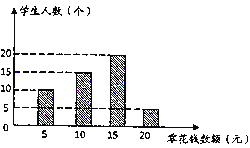
【題目】某教師為了對學(xué)生零花錢的使用進行教育指導(dǎo),對全班50名學(xué)生每人一周內(nèi)的零花錢數(shù)額進行統(tǒng)計調(diào)查,并繪制了統(tǒng)計表及統(tǒng)計圖,如圖所示.
(1)這50名學(xué)生每人一周內(nèi)的零花錢數(shù)額的平均數(shù)是_______元/人;
(2)如果把全班50名學(xué)生每人一周內(nèi)的零花錢按照不同數(shù)額人數(shù)繪制成扇形統(tǒng)計圖,則一周內(nèi)的零花錢數(shù)額為5元的人數(shù)所占的圓心角度數(shù)是_____度;
(3)一周內(nèi)的零花錢數(shù)額為20元的有5人,其中有2名是女生, 3名是男生,現(xiàn)從這5人中選2名進行個別教育指導(dǎo),請用畫樹狀圖或列表法求出剛好選中2名是一男一女的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,方格紙中每個小正方形的邊長都是單位1,△ABC的三個頂點都在格點(即這些小正方形的頂點)上,且它們的坐標(biāo)分別是A(2,﹣3),B(5,﹣1),C(1,3),結(jié)合所給的平面直角坐標(biāo)系,解答下列問題:

(1)請在如圖坐標(biāo)系中畫出△ABC;
(2)畫出△ABC關(guān)于y軸對稱的△A'B'C',并寫出△A'B'C'各頂點坐標(biāo)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,面積為150.
,面積為150.
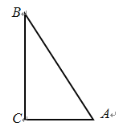
(1)尺規(guī)作圖:作![]() 的平分線交
的平分線交![]() 于點
于點![]() ;(不要求寫作法,保留作圖痕跡)
;(不要求寫作法,保留作圖痕跡)
(2)在(1)的條件下,求出點![]() 到兩條直角邊的距離.
到兩條直角邊的距離.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖為二次函數(shù)![]() 圖象,直線
圖象,直線![]() 與拋物線交于
與拋物線交于![]() 兩點,
兩點,![]() 兩點橫坐標(biāo)分別為
兩點橫坐標(biāo)分別為![]() 根據(jù)函數(shù)圖象信息有下列結(jié)論:
根據(jù)函數(shù)圖象信息有下列結(jié)論:
①![]() ;
;
②若對于![]() 的任意值都有
的任意值都有![]() ,則
,則![]() ;
;
③![]() ;
;
④![]() ;
;
⑤當(dāng)![]() 為定值時若
為定值時若![]() 變大,則線段
變大,則線段![]() 變長
變長
其中,正確的結(jié)論有__________(寫出所有正確結(jié)論的番號)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com