
【題目】如圖,AB是長為10m,傾斜角為37°的自動扶梯,平臺BD與大樓CE垂直,且與扶梯AB的長度相等,在B處測得大樓頂部C的仰角為65°,求大樓CE的高度(結果保留整數).
(參考數據:sin37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() ,sin65°≈
,sin65°≈ ![]() ,tan65°≈
,tan65°≈ ![]() )
)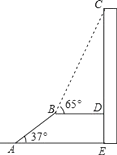
【答案】解:過點B作BF⊥AE于點F.則BF=DE.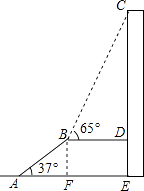
在Rt△ABF中,sin∠BAF= ![]() ∴BF=ABsin∠BAF=10×
∴BF=ABsin∠BAF=10× ![]() =6(m).
=6(m).
又在Rt△CDB中,tan∠CBD= ![]() ,∴CD=BDtan65°=10×
,∴CD=BDtan65°=10× ![]() ≈21(m)
≈21(m)
∴CE=DE+CD=BF+CD=6+21=27(m).
答:大樓CE的高度是27m
【解析】作BF⊥AE于點F.則BF=DE,在直角△ABF中利用三角函數求得BF的長,在直角△CDB中利用三角函數求得CD的長,則CE即可求得.
【考點精析】本題主要考查了關于仰角俯角問題的相關知識點,需要掌握仰角:視線在水平線上方的角;俯角:視線在水平線下方的角才能正確解答此題.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖,PA為⊙O的切線,A為切點,直線PO交⊙O于點E,F過點A作PO的垂線AB垂足為D,交⊙O于點B,延長BO與⊙O交與點C,連接AC,BF.
(1)求證:PB與⊙O相切;
(2)是探究線段EF,OD,OP之間的數量關系,并加以證明;
(3)若tan∠F= ![]() ,求cos∠ACB的值.
,求cos∠ACB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC的垂直平分線分別交AC、BC于E,D兩點,EC=4,△ABC的周長為23,則△ABD的周長為( ) 
A.13
B.15
C.17
D.19
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】要在寬為22米的九州大道AB兩邊安裝路燈,路燈的燈臂CD長2米,且與燈柱BC成120°角,路燈采用圓錐形燈罩,燈罩的軸線DO與燈臂CD垂直,當燈罩的軸線DO通過公路路面的中心線時照明效果最佳,此時,路燈的燈柱BC高度應該設計為( )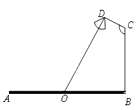
A.![]() 米
米
B.![]() 米
米
C.![]() 米
米
D.![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛經營長途運輸的貨車在高速公路的A處加滿油后,以每小時80千米的速度勻速行駛,前往B地,如表記錄的是貨車一次加滿油后油箱內余油量y(升)與行駛時間x(時)之間的關系:
行駛時間x/時 | 0 | 1 | 2 | 2.5 |
余油量y/升 | 100 | 80 | 60 | 50 |
則y與x的函數關系式為_____,自變量x的取值范圍為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為調查七年級學生了解校園防欺凌知識的情況,小剛在主題班會后就本班學生對校園防欺凌知識的了解程度進行了一次調查統計:A:熟悉,B:較了解,C:知道.如下是他采集數據后,繪制的兩幅不完整的統計圖,請你根據圖中提供的信息解答以下問題:
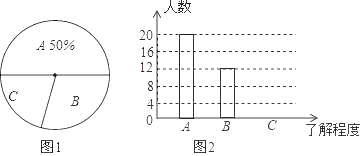
(1)求該班共有多少名學生;
(2)在條形圖中將表示“知道”的部分補充完整
(3)在扇形統計圖中,求“較了解”部分所對應的圓心角的度數;
(4)如果七年級共有460名同學,請你估算全年級對校園防欺凌知識“熟悉”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD的對角線相交于點O,且點O是BD的中點,若AB=AD=5,BD=8,∠ABD=∠CDB,則四邊形ABCD的面積為( )

A.40B.24C.20D.15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A在函數y1=﹣ ![]() (x>0)的圖象上,點B在直線y2=kx+1+k(k為常數,且k≥0)上.若A,B兩點關于原點對稱,則稱點A,B為函數y1 , y2圖象上的一對“友好點”.請問這兩個函數圖象上的“友好點”對數的情況為( )
(x>0)的圖象上,點B在直線y2=kx+1+k(k為常數,且k≥0)上.若A,B兩點關于原點對稱,則稱點A,B為函數y1 , y2圖象上的一對“友好點”.請問這兩個函數圖象上的“友好點”對數的情況為( )
A.有1對或2對
B.只有1對
C.只有2對
D.有2對或3對
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com