【題目】如圖，在在平面直角坐標系xOy中，有一個等腰直角三角形AOB，∠OAB=90°，直角邊AO在x軸上，且AO=1．將Rt△AOB繞原點O順時針旋轉90°得到等腰直角三角形A1OB1，且A1O=2AO，再將Rt△A1OB1繞原點O順時針旋轉90°得到等腰三角形A2OB2，且A2O=2A1O…，依此規律，得到等腰直角三角形A2019OB2019，則點A2019的坐標為_______ ．
【答案】（0，22019）
【解析】
根據題意得出點A的變化規律，進而可得到點A2019的位置及OA2019的長，即可得答案．
∵AO=1，將Rt△AOB繞原點O順時針旋轉90°得到等腰直角三角形A1OB1，且A1O=2AO，再將Rt△A1OB1繞原點O順時針旋轉90°得到等腰三角形A2OB2，且A2O=2A1O…，依此規律，
∴每4次循環一周，A1（0，﹣2），A2（﹣4，0），A3（0，8），A4（16，0），……
∵2019÷4=504……3，
∴點A2019與A3同在y軸正半軸，
∵-2=-21，﹣4=﹣22，8=23，16=24，……，
∴OA2019=22019，
∴點A2019的坐標為（0，22019），
故答案為：（0，22019）
科目：初中數學 來源： 題型：
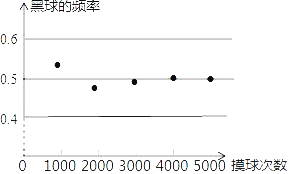
【題目】一個不透明的袋子里裝有黑白兩種顏色的球其40只，這些球除顏色外都相同．小明從袋子中隨機摸一個球，記下顏色后放回，不斷重復，并繪制了如圖所示的統計圖，根據統計圖提供的信息解決下列問題：
（1）摸到黑球的頻率會接近 （精確到0.1）；
（2）估計袋中黑球的個數為 只：
（3）若小明又將一些相同的黑球放進了這個不透明的袋子里，然后再次進行摸球試驗，當重復大量試驗后，發現黑球的頻率穩定在0.6左右，則小明后來放進了 個黑球．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明騎自行車去郊外春游，他離家的距離y（千米）與所用時間x（小時）之間的關系如圖，根據圖象回答：
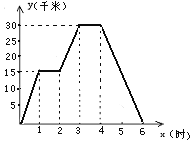
（1）小明到達離家最遠的地方需幾小時？此時離家多遠？
（2）小明出發兩個半小時時離家多遠？
（3）小明出發多長時間離家12.5千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在平面直角坐標系中，已知直線
交
軸于點
，
軸于點
，
的角平分線
交軸于點
，過點作直線
的垂線，交軸于點
．
（1）求直線
的解析式；
（2）如圖2，若點
為直線上的一個動點，過點作
軸，交直線于點
，當四邊形
為菱形時，求
的面積；
（3）如圖3，點
為軸上的一個動點，連接
、
，將
沿
翻折得到
，當以點、
、為頂點的三角形是等腰三角形時，求點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，以點A為中心，把△ABC逆時針旋轉120°，得到△AB'C′（點B、C的對應點分別為點B′、C′），連接BB'，若AC'∥BB'，則∠CAB'的度數為（ ）
A.45°B.60°C.70°D.90°
查看答案和解析>>
科目：初中數學 來源： 題型：
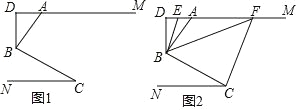
【題目】如圖 1，AM∥CN，點 B 為平面內一點，AB⊥BC 于 B，過 B 作 BD⊥ AM．
（1）求證：∠ABD=∠C；
（2）如圖 2，在（1）問的條件下，分別作∠ABD、∠DBC 的平分線交 DM 于 E、F，若∠BFC=1.5∠ABF，∠FCB=2.5∠BCN，
①求證：∠ABF=∠AFB；
②求∠CBE 的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】課上教師呈現一個問題
甲、乙、丙三位同學用不同的方法添加輔助線解決問題，如下圖：
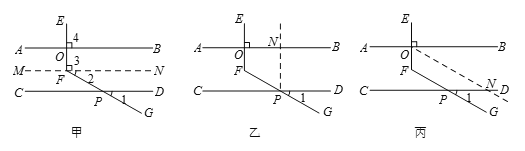
甲同學輔助線的做法和分析思路如下：
（1）請你根據乙同學所畫的圖形，描述輔助線的做法，并寫出相應的分析思路.
輔助線：___________________；
分析思路：
（2）請你根據丙同學所畫的圖形，求∠EFG的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2017年5月，某縣突降暴雨，造成山體滑坡，橋梁垮塌，房屋大面積受損，該省民政廳急需將一批帳篷送往災區．現有甲、乙兩種貨車，已知甲種貨車比乙種貨車每輛車多裝20件帳篷，且甲種貨車裝運1 000件帳篷與乙種貨車裝運800件帳篷所用車輛相等．
(1)求甲、乙兩種貨車每輛車可裝多少件帳篷；
(2)如果這批帳篷有1 490件，用甲、乙兩種汽車共16輛裝運，甲種車輛剛好裝滿，乙種車輛最后一輛只裝了50件，其余裝滿，求甲、乙兩種貨車各有多少輛．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
