
【題目】在正方形![]() 中,
中,![]() ,對角線交于點
,對角線交于點![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() ,將射線
,將射線![]() 繞點
繞點![]() 逆時針轉(zhuǎn)
逆時針轉(zhuǎn)![]() ,交
,交![]() 于點
于點![]() , 則
, 則![]() 的長為____________.
的長為____________.
【答案】![]() 或
或![]()
【解析】
根據(jù)正方形的性質(zhì)得到AC=6![]() ,AC⊥BD,求得AO=BO=
,AC⊥BD,求得AO=BO=![]() ,CP=4
,CP=4![]() ,根據(jù)勾股定理得到PB=
,根據(jù)勾股定理得到PB=![]() ,根據(jù)相似三角形的性質(zhì)即可得到結(jié)論.
,根據(jù)相似三角形的性質(zhì)即可得到結(jié)論.
解:如圖1,
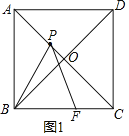
在正方形ABCD中,AB=6,
∴AC=6![]() ,AC⊥BD,
,AC⊥BD,
∴AO=BO=![]() AC=3
AC=3![]() ,
,
∵OP=![]() ,
,
∴CP=4![]() ,
,
在Rt△BPO中,PB=![]() ,
,
∵∠BPF=∠BAP=∠PCF=45°,
∴∠APB=∠PFC=135°-∠FPC,
∴△APB∽△CFP,
∴![]() ,即
,即![]() ,
,
∴PF=![]() ,
,
如圖2,
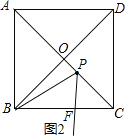
在正方形ABCD中,AB=6,
∴AC=6![]() ,AC⊥BD,
,AC⊥BD,
∴AO=BO=![]() AC=3
AC=3![]() ,
,
∵OP=![]() ,
,
∴CP=2![]() ,
,
在Rt△BPO中,PB=![]() ,
,
∵∠BPF=∠BAP=∠PCF=45°,
∴∠APB=∠PFC=135°-∠FPC,
∴△APB∽△CFP,
∴![]() ,即
,即![]() ,
,
∴PF=![]() ,
,
綜上所述:PF的長為![]() 或
或![]() ,
,
故答案為:![]() 或
或![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知⊙![]() 中,
中,![]() 為直徑,
為直徑,![]() 、
、![]() 分別切⊙
分別切⊙![]() 于點
于點![]() 、
、![]() .
.

(1)如圖①,若![]() ,求
,求![]() 的大小;
的大小;
(2)如圖②,過點![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于點
于點![]() ,交⊙
,交⊙![]() 于點
于點![]() ,若
,若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若一個函數(shù)的解析式等于另兩個函數(shù)解析式的和,則這個函數(shù)稱為另兩個函數(shù)的“生成函數(shù)”。現(xiàn)有關(guān)于x的兩個二次函數(shù)y1、y2,且y1=a(x-m)2+4(m>0),y1、y2的“生成函數(shù)”為:y=x2+4x+14;當(dāng)x=m時,y2=15;二次函數(shù)y2的圖象的頂點坐標(biāo)為(2,k)。
(1)求m的值;
(2)求二次函數(shù)y1、y2的解析式。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是拋物線型拱橋,當(dāng)拱頂離水面![]() 時,水面寬
時,水面寬![]() 為
為![]() .當(dāng)水面上升
.當(dāng)水面上升![]() 時達(dá)到警戒水位,此時拱橋內(nèi)的水面寬度是多少
時達(dá)到警戒水位,此時拱橋內(nèi)的水面寬度是多少![]() ?
?
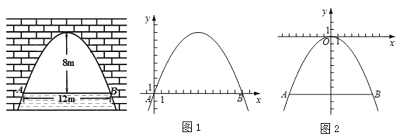
下面給出了解決這個問題的兩種方法,請補充完整:
方法一:如圖1.以點![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,建立平面直角坐標(biāo)系
軸,建立平面直角坐標(biāo)系![]() ,此時點
,此時點![]() 的坐標(biāo)為_______,拋物線的項點坐標(biāo)為_______,可求這條拋物線所表示的二次函數(shù)解析式為_______.當(dāng)
的坐標(biāo)為_______,拋物線的項點坐標(biāo)為_______,可求這條拋物線所表示的二次函數(shù)解析式為_______.當(dāng)![]() 時,求出此時自變量
時,求出此時自變量![]() 的取值,即可解決這個問題.
的取值,即可解決這個問題.
方法二:如圖2,以拋物線頂點為原點,對稱軸為![]() 軸.建立平面直角坐標(biāo)系
軸.建立平面直角坐標(biāo)系![]() ,這時這條拋物線所表示的二次函數(shù)的解析式為_______,當(dāng)水面達(dá)到警戒水位,即
,這時這條拋物線所表示的二次函數(shù)的解析式為_______,當(dāng)水面達(dá)到警戒水位,即![]() _______時,求出此時自變量
_______時,求出此時自變量![]() 的取值為_______,從而得水面寬為
的取值為_______,從而得水面寬為![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
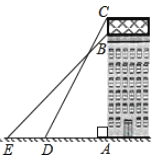
【題目】如圖,一座商場大樓的頂部豎直立有一個矩形廣告牌,小紅同學(xué)在地面上選擇了在條直線上的三點![]() 為樓底),
為樓底),![]() ,她在
,她在![]() 處測得廣告牌頂端
處測得廣告牌頂端![]() 的仰角為
的仰角為![]() ,在
,在![]() 處測得商場大樓樓頂
處測得商場大樓樓頂![]() 的仰角為
的仰角為![]()
![]() 米.已知廣告牌的高度
米.已知廣告牌的高度![]() 米,求這座商場大樓的高度
米,求這座商場大樓的高度![]() (
(![]() ,小紅的身高不計,結(jié)果保留整數(shù)).
,小紅的身高不計,結(jié)果保留整數(shù)).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
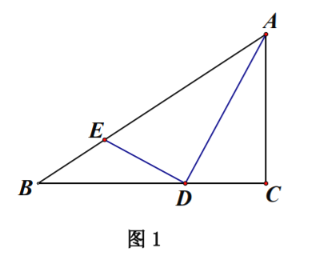
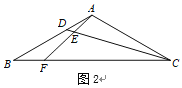
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 、 點
、 點![]() 分別在線段
分別在線段![]() 和線段
和線段![]() 上,
上, ![]() 平分
平分![]() .
.
![]() 如圖1,求證:
如圖1,求證:![]() .
.
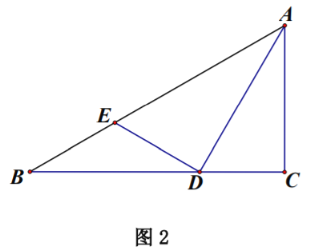
![]() 如圖2,若
如圖2,若![]() .求證:
.求證:![]() .
.
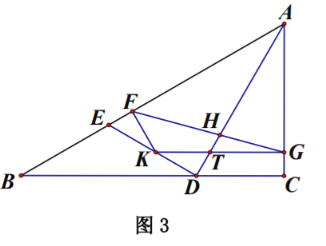
![]() 在
在![]() 問的條件下,如圖3, 在線段
問的條件下,如圖3, 在線段![]() 上取一點
上取一點![]() ,使
,使![]() .過點
.過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,作
,作![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,若
,若![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
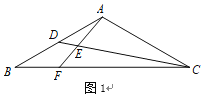
【題目】閱讀下面材料,完成(1),(2)兩題
數(shù)學(xué)課上,老師出示了這樣一道題:如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 上一點,且滿足
上一點,且滿足![]() ,
,![]() 為
為![]() 上一點,
上一點,![]() ,延長
,延長![]() 交
交![]() 于
于![]() ,求
,求![]() 的值.同學(xué)們經(jīng)過思考后,交流了自己的想法:
的值.同學(xué)們經(jīng)過思考后,交流了自己的想法:
小明:“通過觀察和度量,發(fā)現(xiàn)![]() 與
與![]() 相等.”
相等.”
小偉:“通過構(gòu)造全等三角形,經(jīng)過進一步推理,就可以求出![]() 的值.”
的值.”
……
老師:“把原題條件中的‘![]() ’,改為‘
’,改為‘![]() ’其他條件不變(如圖2),也可以求出
’其他條件不變(如圖2),也可以求出![]() 的值.
的值.
(1)在圖1中,①求證:![]() ;②求出
;②求出![]() 的值;
的值;
(2)如圖2,若![]() ,直接寫出
,直接寫出![]() 的值(用含
的值(用含![]() 的代數(shù)式表示).
的代數(shù)式表示).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下面的材料:
如果函數(shù) y=f(x)滿足:對于自變量 x 的取值范圍內(nèi)的任意 x1,x2,
(1)若 x1<x2,都有 f(x1)<f(x2),則稱 f(x)是增函數(shù);
(2)若 x1<x2,都有 f(x1)>f(x2),則稱 f(x)是減函數(shù).
例題:證明函數(shù)f(x)=![]() (x>0)是減函數(shù).
(x>0)是減函數(shù).
證明:設(shè) 0<x1<x2,
f(x1)﹣f(x2)=![]() .
.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴![]() >0.即 f(x1)﹣f(x2)>0.
>0.即 f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函數(shù) f(x)=![]() (x>0)是減函數(shù).
(x>0)是減函數(shù).
根據(jù)以上材料,解答下面的問題:
已知函數(shù)![]() .
.
f(﹣1)=![]() +(﹣2)=-1,f(﹣2)=
+(﹣2)=-1,f(﹣2)=![]() +(﹣4)=
+(﹣4)=![]() .
.
(1)計算:f(﹣3)= ,f(﹣4)= ;
(2)猜想:函數(shù)![]() 是 函數(shù)(填“增”或“減”);
是 函數(shù)(填“增”或“減”);
(3)請仿照例題證明你的猜想.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
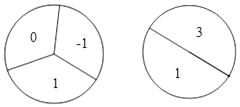
【題目】小明做游戲:游戲者分別轉(zhuǎn)動如圖的兩個可以自由轉(zhuǎn)動的轉(zhuǎn)盤各一次,當(dāng)兩個轉(zhuǎn)盤的指針?biāo)笖?shù)字都為x2﹣4x+3=0的根時,他就可以獲得一次為大家表演節(jié)目的機會.
(1)利用樹狀圖或列表的方法(只選一種)表示出游戲可能出現(xiàn)的所有結(jié)果;
(2)求小明參加一次游戲就為大家表演節(jié)目的機會的概率是多少.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com