
【題目】如圖,在平面直角坐標系xOy中,點A的坐標為(0,3),點B的坐標為(4,0),C為第一象限內一點,AC⊥y軸,BC⊥x軸,D坐標為(m,0)(0<m<4).
(1)若D為OB的中點,求直線DC的解析式;
(2)若△ACD為等腰三角形,求m的值;
(3)E為四邊形OACB的某一邊上一點.
①若E在邊BC上,滿足△AOD≌△DBE,求m的值;
②若使△EOD為等腰三角形的點E有且只有4個,直接寫出符合條件的m的值.
【答案】(1) y=![]() x﹣3;(2)2或
x﹣3;(2)2或![]() 或4-
或4-![]() ;(3)①1;②4或
;(3)①1;②4或![]()
【解析】
(1)求出C、D兩點坐標,利用待定系數法即可解決問題;
(2)分三種情形討論求解即可;
(3)①利用全等三角形的性質可知OA=BD=3;
②當m=3或![]() 時,使△EOD為等腰三角形的點E有且只有4個.
時,使△EOD為等腰三角形的點E有且只有4個.
(1)∵A(0,3),B(4,0),四邊形AOBC是矩形,
∴OA=BC=3,OB=AC=4,
∴C(4,3),
∵點D為OB中點,
∴D(2,0),
設直線CD的解析式為y=kx+b,則有![]() ,
,
解得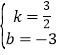 ,
,
∴直線CD的解析式為y=![]() x﹣3.
x﹣3.
(2)①當DA=DC時,D(2,0).
②當AD=AC=4時,在Rt△AOD中,OD=![]() ,
,
∴D(![]() ,0).
,0).
③當CD=AC時,在Rt△BCD中,BD=![]() ,
,
∴D(4﹣![]() ,0).
,0).
(3)①∵△AOD≌△DBE,
∴DB=OA=3,
∴OD=OB﹣BD=1,
∴m=1.
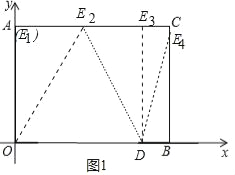
②如圖1中,當m=3時,使△EOD為等腰三角形的點E有且只有4個;
如圖2中,當E與C重合時,OD=DC=m,
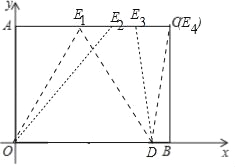
在Rt△CDB中,∵CD2=BD2+BC2,
∴m2=(4﹣m)2+32,'
∴m=![]() .此時使△EOD為等腰三角形的點E有且只有4個.
.此時使△EOD為等腰三角形的點E有且只有4個.


科目:初中數學 來源: 題型:
【題目】“十一”長假期間,小張和小李決定騎自行車外出旅游,兩人相約一早從各自家中出發,已知兩家相距10千米,小張出發必過小李家.
(1)若兩人同時出發,小張車速為20千米,小李車速為15千米,經過多少小時能相遇?
(2)若小李的車速為10千米,小張提前20分鐘出發,兩人商定小李出發后半小時二人相遇,則小張的車速應為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知∠AOB=45°,點P在∠AOB內部,點P1與點P關于OA對稱,點P2與點P關于OB對稱,連接P1P2交OA、OB于E、F,若P1E=![]() ,OP=
,OP=![]() ,則EF的長度是_____.
,則EF的長度是_____.
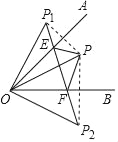
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某路段某時段用雷達測速儀隨機監測了200輛汽車的時速,得到如下頻數分布表(不完整):注:30﹣40為時速大于或等于30千米而小于40千米,其它類同.
數據段 | 頻數 |
30~40 | 10 |
_______ | 36 |
50~60 | 80 |
60~70 | _____ |
70~80 | 20 |
(1)請你把表中的數據填寫完整;
(2)補全頻數分布直方圖;
(3)如果此路段該時間段經過的車有1000輛.估計約有多少輛車的時速大于或等于 60千米.
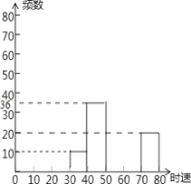
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道分數![]() 寫為小數即
寫為小數即![]() ,反之,無限循環小數
,反之,無限循環小數![]() 寫成分數即
寫成分數即![]() .
.
一般地,任何一個無限循環小數都可以寫成分數形式.
例如:把![]() 寫成分數形式時,設
寫成分數形式時,設![]() =
=![]() ,則
,則![]() =0.5555…=0.5+0.05555…=
=0.5555…=0.5+0.05555…=![]()
解一元一次方程![]() ,解得:
,解得:![]() ,所以
,所以![]() =
=![]() .
.
(1)模仿上述過程,把無限循環小數0.![]() 寫成分數形式;
寫成分數形式;
(2)你能把無限循環小數![]() 化成分數形式嗎?
化成分數形式嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】元旦晚會上,王老師要為她的學生及班級的六位科任老師送上賀年卡,網上購買賀年卡的優惠條件是:購買50或50張以上享受團購價.王老師發現:零售價與團購價的比是5:4,王老師計算了一下,按計劃購買賀年卡只能享受零售價,如果比原計劃多購買6張賀年卡就能享受團購價,這樣她正好花了100元,而且比原計劃還節約10元錢;
(1)賀年卡的零售價是多少?
(2)班里有多少學生?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com